Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 211
A barra esbelta uniforme de massa e comprimento é livremente articulada em torno de um eixo horizontal por meio de sua extremidade e recebe uma velocidade angular inicial quando cruza a posição vertical onde . Se a barra oscila através de um ângulo máximo , desenvolva uma expressão na forma integral para o tempo desde a liberação em até ser atingido. (Expresse em termos de ).
Passo 1
Uma barra gira ao redor de um pino em uma de suas extremidades. A barra vai de uma posição vertical até um certo ângulo .
Queremos descobrir quanto tempo passou da posição até
Dados da questão (tudo conhecido!):
- Massa:.
- Comprimento: .
- Ângulo inicial: .
- Ângulo final: .
- Velocidade inicial: .
- Velocidade final: (em !)
Vamos analisar a dinâmica do problema e aí procuramos isolar de algum jeito. A questão já nos deu a dica que a solução vai ser uma expressão para na forma integral.
Passo 2
A barra está girando ao redor do pino em sentido horário. Defina eixos com direção positiva. A única força no problema é o próprio peso da barra, que age no centro de massa, no meio dela.
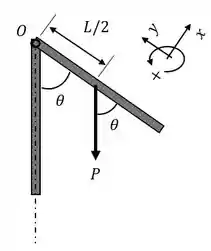
A componente de que importa para a rotação é a que está na direção :
Aplicando a segunda Lei de Newton na forma angular para o ponto , temos
Beleza, temos uma expressão envolvendo e . Só precisamos dar uma ajeitada nela para isolar o .
Esse na equação é o momento de inércia em relação ao ponto !
Voltando a equação da dinâmica, substitua e .
Vamos simplificar e escrever cada derivada no tempo como um ponto.
Beleza, temos uma expressão que relaciona a aceleração com a posição. O que acontece se integrarmos em relação à posição ?
Passo 3
Agora vem a sacada principal. Vamos usar a regra da cadeira para avaliar a derivada da velocidade em relação à posição .
Como a função nessa questão é inversível (só há um valor de para cada !), podemos dizer que
E aí achamos algo bem interessante ao substituir:
Agora podemos mexer um pouco os diferenciais para termos integrais que conseguimos calcular
Integre da posição inicial ) até uma posição genérica . A velocidade no início é e na posição genérica ela vai ser algum valor .
O é conhecido, mas a questão pede que expressemos ele em termos de . Podemos usar essa equação para isso. Aplique a informação que temos: quando , a velocidade é
Ótimo, agora vamos colocar essa expressão de de volta na equação que achamos!
Mas e daí? Achamos uma expressão que relaciona a velocidade angular com o ângulo. Bem, como a velocidade é a derivada do ângulo no tempo, dá pra gente reverter isso aí e achar o !
Passo 4
Definição da velocidade:
Isole o !
Agora é só substituir e integrar! Integre do instante inicial até o final . O ângulo vai ser no início e no final
Resposta
Tempo de até .