Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.3 - Ex. 66
A peça anexa recebe um movimento horizontal . Desenvolva a equação do movimento para a massa e determine a frequência crítica para a qual as oscilações da massa tornam-se excessivamente grandes. Qual o fator de amortecimento do sistema?
Passo 1
Dados da questão:
- Massa: .
- Rigidez da mola:
- Coeficientes de amortecimentos: e .
- Movimento da extremidade direita do amortecedor : .
Queremos uma equação que defina o movimento da massa com todos esses elementos interagindo. Vai ser bem tranquilo! Primeiro passo vai ser identificar quem são as forças atuando na massa, e aí vamos identificar cada força.
Depois a gente vai procurar a frequência que faz as oscilações serem extremamente grandes e o fator de amortecimento.
Passo 2
Escolha uma posição de referência e aí tome um deslocamento qualquer. A partir disso a gente desenha o diagrama de corpo livre.
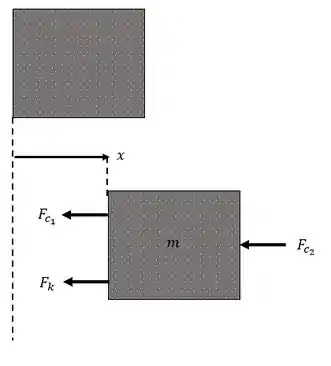
Beleza! Quando a massa vai para a direita, a mola e os dois amortecedores vão gerar forças para esquerda, porque eles resistem ao movimento.
Agora a gente escreve a equação da dinâmica para a massa :
A aceleração vai ser a segunda derivada do deslocamento no tempo: . Coloque as forças externas na equação. Atenção ao sinal! Elas estão em sentido oposto ao deslocamento .
Vamos ver quem é cada uma dessas forças, e ir conferindo se a direção das forças no diagrama de corpo livre está certa!
Passo 3
Vejamos a mola com rigidez . A mola resiste à deflexão dela! Isso significa que se uma extremidade da mola se afastar da outra, a mola vai puxar ela de volta pro comprimento natural. Essa resistência é a força que a mola gera, linear à variação de comprimento!
A extremidade esquerda da mola está fixa. A massa vai para direita um comprimento . A extremidade direita dessa mola vai se mover para direita!
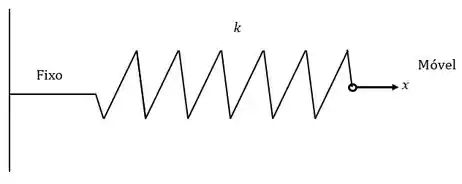
Como a mola é estendida para direita um comprimento , a força que resiste isso vai para esquerda! Show, isso confere com o Passo .
Passo 4
Para a força devida ao amortecedor, ela será linear à velocidade do pistão dentro dele. Vejamos o amortecedor com coeficiente .
A velocidade da massa é , e se o corpo está indo para direita, então também aponta para direita! Como a extremidade esquerda desse amortecedor está fixa, o pistão vai ter a mesma velocidade !
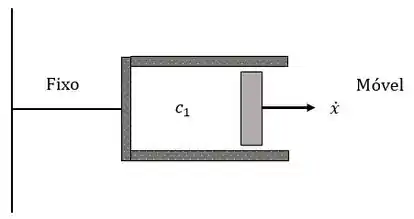
A velocidade é para direita, então a força que resiste isso tem que ir para esquerda! Beleza, de novo correto com o Passo !
Passo 5
Aqui vem a parte mais importante! O amortecedor de coeficiente vai ter seu pistão movido para direita a uma velocidade : a velocidade que a massa está indo para direita. Mas outra coisa vai acontecer também. A base do amortecedor, na direita, vai se mover também para direita! Esse movimento é , então ele ocorre a uma velocidade .
Lembre-se que falamos que o amortecedor gera uma força para resistir a variação de velocidade do pistão. Então não interessa se o amortecedor com ou todo se move, o que importa é o aumento de velocidade do pistão dele.
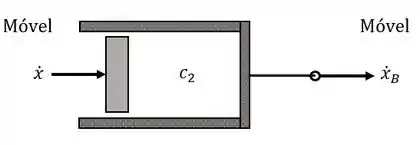
A velocidade relativa do pistão vai aumentar
Isso é o quanto o pistão aumenta em velocidade para direita! Então o amortecedor resiste com uma força para esquerda! Essa força vai ser
Ótimo! Queríamos uma força para esquerda mesmo (Passo ). Fique atento que se você pensar na outra direção, muda tudo!
Agora é só botar de volta na equação principal e mexer umas coisinhas.
Passo 6
Vamos colocar a expressão , e além disso vamos agrupar os termos em relação a e suas derivadas.
Show, achamos a equação!
Passo 7
E qual é a frequência crítica que deve assumir para causar grandes oscilações? Essa frequência é a que gera ressonância!
Ressonância acontece quando a frequência do forçamento se aproxima da frequência natural do sistema.
Resta descobrirmos quem é para esse sistema então. Isso é bem fácil!
Apesar da equação do Passo ser ligeiramente diferente da equação que você está acostumado, você pode imaginar que na verdade o que temos ali é um coeficiente e amortecimento equivalente e um forçamento harmônico em que a amplitude é .
Relembre a equação habitual
Para fazemos nossa equação ficar nessa forma, só precisamos dividir por !
Comparando,
Passo 8
Quase lá! E qual é o fator de amortecimento ? Compare as equações no último Passo!
Substitua a expressão do :
Resposta
Equação do movimento:
Frequência de ressonância:
Fator de amortecimento: