Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 94
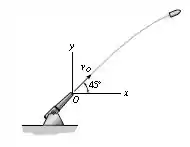
O projétil de massa é disparado de um canhão a uma velocidade na boca do canhão . Determine a quantidade de movimento angular do projétil em relação ao ponto no instante que ele está na altura máxima de sua trajetória.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Temos que, no ponto onde a altura é máxima, o projétil viaja somente com a velocidade horizontal, dada por:
Agora vamos descobrir a altura máxima do projétil:
A quantidade de movimento angula é dada por:
Resposta
Exercícios de Livros Relacionados
As Figuras (1) e (2) mostram como molas podem ser usadas para suportar um bloco em duas situações diferentes. Na Fig. (1), elas ajudam a diminuir a amplitude da força oscilante transmitida pelo blocoà
Em um sistema com amortecimento subcrucial (c c c ), o período de vibração é usualmente definido como o intervalo de tempo τ d = 2π / ω d correspondente a dois pontos sucessivos onde a curva deslocame
Na prática, é frequentemente difícil determinar o decremento logarítmico de um sistema com o amortecimento subcrucial definido no Problema 19.129 pela medida de dois deslocamentos máximos sucessivos.
Mostre que, no caso de amortecimento supercrucial (c c c ), um corpo liberado de uma posição arbitrária com uma velocidade inicial arbitrária não pode passar mais de uma vez pela sua posição de equilí
Um disco de 30 kg é fixado, com uma excentricidade e = 0,15 mm,ao ponto médio de um eixo vertical AB que gira com uma velocidadeangular ω ƒ ƒ constante. Sabendo que a constante de mola k para o movime