Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 103

A barra AB é feita de um aço doce considerado elastoplástico com E = 200   G P a   e     σ E = 248   M P a . Depois de a barra ter sido lixada a uma alavanca rígida CD, descobriu-se que a extremidade C está 9,53 mm mais alta do que deveria estar. Uma força vertical Q é aplicada a C até que esse ponto se mova para posição C. Determine a intensidade necessária de Q e o deslocamento δ 1 para que a alavanca volte para a posição horizontal depois que Q for removida.

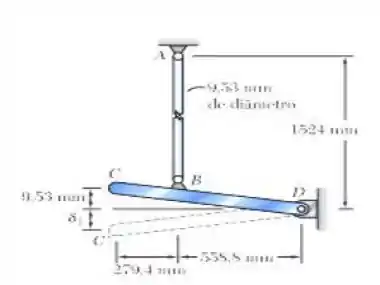
Passo 1

Fala aí gurizada tudo belezinha? O enunciado pede para a gente determinar a intensidade necessária de Q e o deslocamento δ 1 para que a alavanca volte para a posição horizontal depois que Q for removida, parece complexo ne? Mas calma, vem comigoo !!!

Primeiramente vamos calcular a área :D

A A B = π 4   x   9 2 = 63,617   m m ² = 63,617   x   10 - 6 m ²

Uma vez que a haste AB deve ser esticada permanentemente, temos que determinar a força :D F A B m a x = A A B σ y = 63,617   x   10 - 6   x   345   x   10 - 6 = 21,948   x   10 3 N

Passo 2

Agora galera temos que determinar o somatório do momento em D vem comigo :D

+ ∑ M D = F x d = 0

        1,1 Q - 0,7 F A B = 0

Q m a x = 0,7 1,1   x   21,948   x   10 3 = 13,9669   x   10 - 3 N

Então o alongamento em AB temos... δ ' A B = F A B m a x L A B E A A B = 21,948   x   10 3   x   1,25 200   x   10 9   x   63,617   x   10 - 6 = 2,15625   x   10 - 3 m

E o ângulo desta mudança de posição da alavanca é de: θ ' = δ A B ' 0,7 = 3,0804   x   10 - 3 r a d

E o deslocamento δ 1 para que a alavanca volte para a posição horizontal é dada por: δ 1 = 1,1 θ ' = 3,39   x   10 - 3 m

Resposta

13,97   k N 3,39   m m  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um arame de aço de 60 m de comprimento não deve alongar-se mais do que 48 m m , quando é aplicado uma tração de 6 k N . SendoE = 200G P a , determinar:O menor diâmetro que pode ser especificado para o
Um arame de 80 m de comprimento e diâmetro de 5 m m é feito de um aço com E = 200G P a e tensão última de 400M P a . Se um coeficiente de segurança de 3,2 é desejado, qual é:A maior tração admissível
Resolver o P r o b .2.58 , considerando que a porção AB da barra composta é de latão e a porção BC de aço.
Uma barra composta de duas porções cilíndricas AB e BC é engastada em ambas as extremidades. A porção AB é de aço ( E = 200G P a ; α = 11,7.10 - 6 ° C - 1 ) e a porção BC é de latão ( E = 105G P a ; α
A barra AB é de latão ( E = 105G P aeα = 20,9.10 - 6° C - 1 ) e a barra CD de alumínio ( E = 70G P aeα = 23,6.10 - 6° C - 1 ). Sabendo-se que a 16°C a fenda existente entre as extremidades das barras