Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 59
Resolver o , considerando que a porção AB da barra composta é de latão e a porção BC de aço.
Passo 1
Queremos determinar tensões e deformações em uma estrutura que deforma por variação de temperatura, e sabemos que para determinarmos isso, precisamos determinar forças, e para determinar forças precisamos determinar diagramas, então vamos lá, vamos começar pelo diagrama:
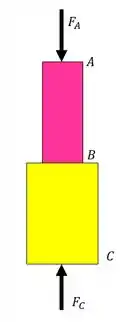
Mas agora precisamos de uma equação de compatibilidade para podermos resolver o nosso problema. Perceba que a deformação total entre os pontos A e C tem que ser igual a zero no somatório de deformações, e que teremos deformações devido a temperatura e devido aos normais que aparecem nas paredes, dessa forma teremos que:
Em que:
E sabemos que os dados do enunciado são dados por:
E agora só precisamos determinar os normais relacionados com as forças que queremos descobrir.
Passo 2
Usando o nosso diagrama teremos que:
- Trecho AB
- Trecho BC
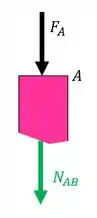
Sendo assim teremos que:
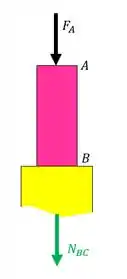
Sendo assim teremos que:
Substituindo na nossa fórmula teremos que:
Passo 3
Se temos a força podemos definir as tensões normais, que é a força dividido pela área da seção, sendo assim teremos que:
- Barra AB
- Barra BC
E sabemos que para determinar o deslocamento do ponto B precisamos escolher uma das duas barras ( e tanto faz qual, porque lembra que o somatório de deformações total dava zero) e fazer a diferença entre o que essa barra deformou devido a força e devido a temperatura, então se eu escolher a barra AB, teremos que: