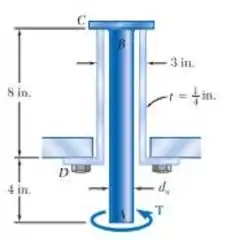
O sistema da figura é constituído por um eixo de aço com seção transversal cheia AB, com diâmetro e tensão de cisalhamento admissível de 82 MPa, e por um tubo CD feito de latão com uma tensão de cisalhamento admissível de 48 MPa. Determine o maior torque T que pode ser aplicado em A .
Passo 1
E aí galerinha neste exercício precisamos analisar primeiramente o torque exercido sobre o eixo AB.
Para determinarmos o torque precisamos determinar a partir da equação a seguir:
Gurizada notem que as medidas do elemento foram dadas em unidades americanas e as tensões em SI, então precisamos decidir se mudamos as dimensões para m ou as tensões para ksi, notem que é mais rapidinho transformar as tensões em ksi. Então temos:
82 MPa = 11, 9 ksi
Passo 2
Então agora vamos analisar o trecho CD do perfil em L :
Onde J é determinado por:
Para determinar o torque temos que aplicar na equação a seguir:
Resposta
E por fim o menor toque exercido sobre o ponto A.