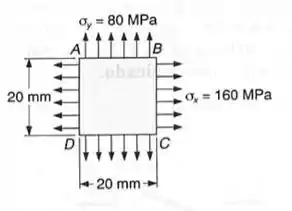
Um quadrado de de lado é desenhado na parede de um vaso de pressão de aço de grandes dimensões. Depois de pressurizado o estado biaxial de tensões no quadrado é como o mostrado. Usando a tabela do apêndice B, para o aço estrutural, determinar a variação do comprimento:

1. Do lado AB;
2. Do lado BC;
3. Da diagonal AB.

A questão nos pede algumas informações, como por exemplo a deformação longitudinal de AB, de BC e da diagonal BD, e para isso o nosso enunciado nos dá os seguintes dados.

Assim o coeficiente de Poisson será dado por:

Usando a lei de Hooke generalizada, teremos a seguinte a fórmula:

Agora olhando cada um de cada vez teremos que:

1. Deformação na direção AB (direção x)

Sabemos que:

Substituindo teremos que:

2. Deformação na direção BC (direção y)

Sabemos que:

Substituindo teremos que:

3. Deformação na diagonal BD

Nesse vamos precisar fazer uma analise de derivadas, para isso podemos usar a seguinte conta:

Que seria como se estivéssemos determinando as diagonais a partir dos lados, como queremos uma variação, podemos fazer a seguinte derivada:

Dividindo tudo por 2 teremos que:

Sabemos que “a” e “b” são os lados do quadrado que podemos escrever como:

Sabemos também que “c” é o tamanho da diagonal, e com isso podemos escrever que:

E sabemos quanto foi a variação dos lados “a” e “b”, sendo assim teremos que:

Substituindo na equação teremos que: