Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 69

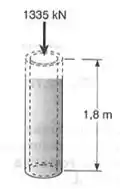
Um tubo de aço de 1,8 m de comprimento, 300 m m de diâmetro externo e 13 m m de espessura é usado como uma pequena coluna e suporta uma carga axial centrada de 1335   k N . Usando a tabela do apêndice B, para aço estrutural, determinar:

  1. A variação de comprimento do tubo;
  2. A variação do diâmetro externo do tubo;
  3. A variação da espessura da parede do tubo.

Passo 1

A questão nos pede algumas informações, como por exemplo a deformação longitudinal, de diâmetro e de espessura, e para isso o nosso enunciado nos dá os seguintes dados.

L = 1,8 m = 1800   m m

D e x t e r n o = 300   m m

D i n t e r n o = 300 - 13 - 13 = 274

e = 13   m m

P = - 1335   k N   ( c o m p r e s s ã o )

E = 200   G P a

ϑ = 0,30

A = π 4 D e 2 - D i 2 = π 4 300 2 - 274 2 = 11721   m m 2

Agora olhando cada um de cada vez teremos que:

  1. Deformação longitudinal (usando a lei de Hooke)

    2. ε = σ E

    ε = δ L

    σ = N A

    Substituindo teremos que:

    δ L = N A E

    δ = N L E A

    Substituindo os valores teremos que:

    δ = N L E A = - 1335   .   1800 200   .     11721 = - 1,025   m m

    δ = - 1,025   m m   ( r e d u ç ã o   d e   c o m p r i m e n t o )

  2. Deformação Diâmetro externo (Coeficiente de Poisson)

    3. ε D = - ϑ ε

    Sabemos que:

    ε D = δ D D

    ε = δ L

    Substituindo teremos que:

    ε D = - ϑ ε

    δ D D = - ϑ δ L

    δ D = - ϑ D δ L

    Substituindo teremos que:

    δ D = - 0,30   .   300   . - 1,025 1800 = 0,05125   m m = 5,125   .   10 - 2 m m    

  3. Deformação espessura (Coeficiente de Poisson)

ε e = - ϑ ε

Sabemos que:

ε e = δ e e

ε = δ L

Substituindo teremos que:

ε e = - ϑ ε

δ e e = - ϑ δ L

δ e = - ϑ e δ L

Substituindo teremos que:

δ e = - 0,30   .   13   . - 1,025 1800 = 0,002221   m m = 2,221   .   10 - 3 m m    

Resposta

  1. δ = - 1,025   m m   ( r e d u ç ã o   d e   c o m p r i m e n t o )
  2. δ D = 5,125   .   10 - 2 m m    
  3. δ e = 2,221   .   10 - 3 m m    
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Levando em conta apenas o efeito das tensões normais, determine a energia de deformação da viga prismática AB para o carregamento mostrado.
E = 10,5 × 10 6 p s i . Determine a energia de deformação da treliça para o carregamento mostrado.
Levando em conta apenas o efeito das tensões normais, determine a energia de deformação da viga prismática AB para o carregamento mostrado.
Usando E = 200G P a , determine a energia de deformação devido à flexão para a barra de aço e o carregamento mostrado. (Desconsidere os efeitos das tensões de cisalhamento.)
Usando E = 200G P a , determine a energia de deformação devido à flexão para a barra de aço e o carregamento mostrado. (Desconsidere os efeitos das tensões de cisalhamento.)