Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 179
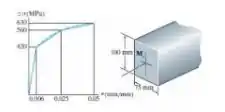
A barra é feita de uma liga de alumínio cujo diagrama tensão – deformação pode ser aproximada pelos segmentos de reta mostrados na figura. Considerando que esse diagrama é o mesmo para tração e compressão, determine o momento que a barra suportará se a deformação máxima nas fibras superiores e inferiores da viga for εmáx = 0,05.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que tem essa viga tem uma esse formato de um retângulo, e nos pede o momento para que a deformação seja aquela lá dada. Partiu??
Passo 2
Ok, nós vamos começar pensando na barra. Vamos achar quanto vale a tensão máxima suportada pela viga. Antes disso, vamos analisar os pontos em que há uma alteração na estrutura da tensão; esses pontos serão onde há a mudança na inclinação da reta do nosso diagrama, certo??
Com as nossas posições já encontradas, vamos achar nossas tensões equivalentes para cada uma dessas posições.
Passo 3
Pronto!! Agora vamos jogar tudo lá na nossa formulinha e teremos o nosso momento.