Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 86

A viga é composta por quatro tábuas coladas ao longo das linhas de junção. Se a cola puder resistir a 15 kN/m e a viga sofrer uma rotação de 90°, qual é o cisalhamento vertical máximo V que a viga pode suportar?

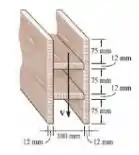
Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que tem essa viga tem uma esse formato estranho, e nos pede o cisalhamento máximo. Partiu??

Passo 2

Ok, nós vamos começar pensando na barra. Vamos pensar juntos com relação à linha neutra. Dela até o centro das nossas barrinhas laterais, temos uma distância de:

d = 0,0435   m

Agora que já sabemos disso, podemos calcular nosso I.

I = 2 0,012   x   0,1 3 12 + 2   0 , 249   x   0,012 3 12 + 0 , 249   x   0,012   x   0,0 56 2 = 2,081245   x   10 - 5   m 4

Pronto, com o nosso momento de inércia calculado, vamos achar o nosso fluxo de cisalhamento.

Q = A ' y ' = 0 , 249   x   0,012 0,05 6 = 1,67328   x   10 - 4   m 3    

Passo 3

Pronto!! Agora vamos jogar tudo lá na nossa formulinha e teremos a nossa tensão de cisalhamento e, consequentemente, o nosso cortante.

q = V Q 2 I

15 = V 1,67328   x   10 - 4 2   x   2,081245   x   10 - 5

V = 3,731   k N

Resposta

V = 3,731   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Faça um gráfico da intensidade da tensão de cisalhamento distribuída na seção transversal da escora se ela for submetida a uma força de cisalhamento V = 15 k N .
A viga é composta por três tábuas coladas nas linhas de junção A e B. Se for submetida ao carregamento mostrado na figura, determine a tensão de cisalhamento desenvolvida nas juntas coladas na seção a
A viga está sujeita a uma carga uniforme w. Determine a localização a dos apoios de modo que a tensão de cisalhamento na viga seja a menor possível. Qual é essa tensão?
As extremidades da viga de madeira devem ser entalhadas como mostra a figura. Se a viga tiver de suportar o carregamento mostrado, determine a menor profundidade d da viga no entalhe se a tensão de ci
A viga T está sujeita ao carregamento mostrado na figura. Determine a tensão de cisalhamento transversal máxima na seção crítica da viga.