Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 5.Problemas - Ex. 81
69. A barra está fixada por três mancais radiais lisos em e . Determine as componentes da reação nesses mancais.
Passo 1
Faala galerinha, bonita, tudo beleza?? Saca só, o enunciado nos deu uma barra fixada por três mancais radiais lisos em , e como na figura abaixo:
E sabendo que o sistema deve estar em equilíbrio, o enunciado quer que a gente determine as forças de reação em cada mancal. Então pra isso, primeiro devemos esboçar o diagrama de corpo livre pra barra com as forças em cada mancal, que será dado como:
Como as forças nos mancais já conseguem impedir que a montagem gire em relação a cada eixo de coordenada, os mancais exercem apenas forças reativas.
Passo 2
Iradoso, agora que temos o diagrama de forças podemos começar a determinar cada uma delas através das equações do equilíbrio. Por exemplo, no eixo devemos ter:
Como temos apenas e uma força de no eixo , vamos obter que:
Agora se a gente fizer o somatório dos momentos no eixo , vamos obter:
De modo que:
Logo:
Maravilha, já descobrirmos os valores das reações em .
Passo 3
Agora pra gente determinar as reações em , vamos usar a malandragem e traçar um eixo como na figura:
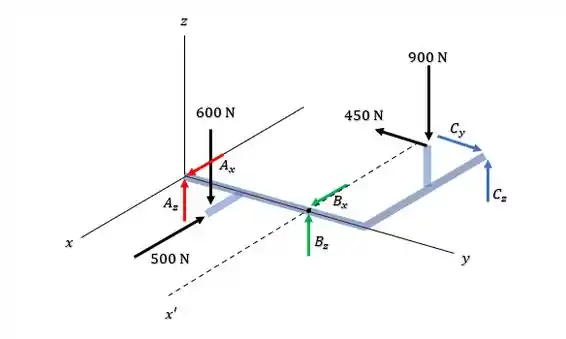
E agora se a gente calcular o momento em relação a esse eixo, vamos obter que:
Logo:
Passo 4
Vamos usar a equação referente ao momento em , para achar :
Sendo assim:
Agora vamos usar a equação referente ao momento em , para achar :
Logo:
E por fim, vamos usar a equação referente a força em , para acharmos a última incógnita :