Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 120

Resolver o Problema 2.119 admitindo que um terceiro operário esteja exercendo uma força P → = - 178   N i → no contrapeso.

Passo 1

Podemos escrever o somatório de forças no ponto A com o auxílio da figura a seguir como:

∑ F → A = 0

T → A B + T → A C + N → - W j → - P i → = 0

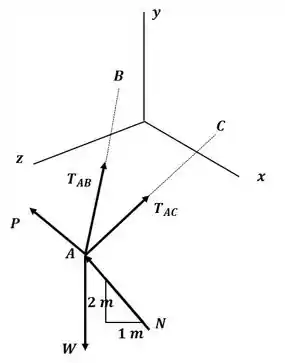
Agora precisamos escrever os vetores tensão e o vetor normal em termos de suas coordenadas, para isso, precisamos primeiro escrever o vetor que liga esses pontos, então:

A B → = - 1 i → + 1,8 j → - 1 k →

A C → = 1,1 i → + 1,5 j → - 1 k →

N → = 2 j → + 1 k →

Agora, calculando o módulo desses vetores:

A B = - 1 2 + 1,8 2 + - 1 2 → A B = 2,29   m

A C = 1,1 2 + 1,5 2 + - 1 2 → A C = 2,11   m

N = 0 2 + 2 2 + 1 2 → N = 2,24   m

Agora podemos escrever os vetores tensão e normal como:

T → A B = T A B . A B → A B = T A B - 0,437 i → + 0,786 j → - 0,437 k →

T → A C = T A C . A C → A C = T A C 0,521 i → + 0,711 j → - 0,474 k →

N → = N . N → N = N 0 i → + 0,893 j → + 0,446 k →

Passo 2

Agora substituindo os valores das tensões na equação de equilíbrio de forças do passo 1, temos:

T A B - 0,437 i → + 0,786 j → - 0,437 k → + T A C 0,521 i → + 0,711 j → - 0,474 k → + N 0 i → + 0,893 j → + 0,446 k → - W j → - P i → = 0

Agora vamos separar as componentes i → ,   j → e k → :

- 0,437 T A B + 0,521 T A C - P = 0

0,786 T A B + 0,711 T A C + 0,893 N - W = 0

- 0,437 T A B - 0,474 T A C + 0,446 N = 0

Agora, substituindo o valor de W dado no enunciado, as equações se tornam:

- 0,437 T A B + 0,521 T A C - 178 = 0

0,786 T A B + 0,711 T A C + 0,893 N - 890 = 0

- 0,437 T A B - 0,474 T A C + 0,446 N = 0

Passo 3

Agora, isolando T A B da terceira equação:

T A B = - 1,085 T A C + 1,02 N

E, susbtituindo esse valor nas equações 1 e 2:

- 0,437 - 1,085 T A C + 1,02 N + 0,521 T A C - 178 = 0 → T A C = 0,448 N + 178,9

0,786 - 1,085 T A C + 1,02 N + 0,711 T A C + 0,893 N - 890 = 0 → N = 0,0837 T A C + 525,2

Substituindo esse valor na equação anterior:

T A C = 0,448 0,0837 T A C + 525,2 + 178,9 → T A C = 430,3   N

Substituindo esse valor na equação para N :

N = 0,0837 430,3 + 525,2 → N = 561,2   N

Agora, substituindo o valor de T A C na primeira equação do passo 2:

- 0,437 T A B + 0,521 545,7 - 178 = 0 → T A B = 243,3   N

Resposta

T A B = 243,3   N

T A C = 430,3   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tipo de batente de porta pequeno e ajustável que se encaixa nos pinos da dobradiça é mostrado na figura. A porta é mostrada fechada na visualização normal e aberta na visualização ampliada do baten
Um grande tambor simétrico para secar areia é operado pelo motor de engrenagens mostrado. Se a massa da areia for 750k g e uma força média do dente da engrenagem de 2,6k N for fornecida pelo pinhão do
Três bolas de aço idênticas, cada uma com massa m , são colocadas no anel cilíndrico que se apóia sobre uma superfície horizontal e cuja altura é ligeiramente maior que o raio das bolas. O diâmetro do
O suporte da polia é preso à sua fundação por dois parafusos B e dois parafusos C com uma tensão inicial em cada um dos quatro parafusos antes da aplicação da tensão 500N no cabo. Determine o aumento
A unidade de energia da escavadeira pós-furo fornece um torque de 4000l b ∙ i n para a broca. O braço B está livre para deslizar na manga de suporte C , mas não está livre para girar em torno do eixo