Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 153
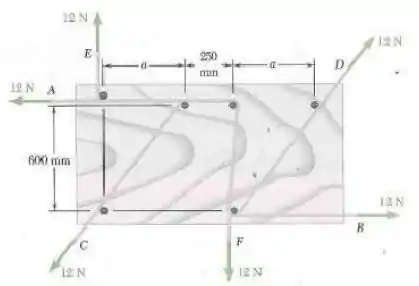
Uma cablagem é feita pela passagem de dois ou três fios em torno de cavilhas de diâmetro montadas em uma placa de compensado de madeira. Se a força de cada fio é , determine o binário resultante exercido no compensado de madeira quando apenas os fios e estão no lugar, todos três fios estão no lugar.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
A questão nos pede o binário (momento) resultante exercido no compensado de madeira.
Encontramos o binário resultante por:
Para o item a, considerando somente as cordas e , temos:
Estas distâncias são as perpendiculares entre as linhas de ação das forças. Outro ponto que devemos ter cuidado é com o diâmetro das cavilhas, pois eles aumentam a distância.
A distância , por exemplo, será:
Pois a corda passa pelo furo superior e pelo inferior, o que nos fez considerar metade do diâmetro em cada furo que a corda passou.
Passo 2
Lembre-se que queremos a distância perpendicular à linha de ação da força.
Fiz esses diagramas pra gente poder visualizar melhor:
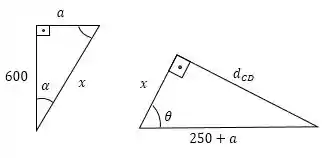
Podemos obter o valor de , a partir do teorema de Pitágoras para o primeiro triângulo:
Agora, observe uma coisa interessante. Temos que o ângulo e devem ser complementares, portanto:
Utilizaremos esse recurso para descobrir :
Portanto:
Encontramos esse valor, mas sabemos que devemos considerar também o diâmetro das cavilhas. Portanto:
Passo 3
Agora é só calcular:
Passo 4
Item b:
Se considerarmos adicionar a corda , temos que:
A distância perpendicular à linha de ação da força será:
Logo: