Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 34
Desprezando o atrito, determine a tração no cabo ABD e a reação em C quando .
Passo 1
Tá legal, vamos lá! A primeira coisa que fazemos nesse tipo de exercício é desenhar o DCL do sistema:
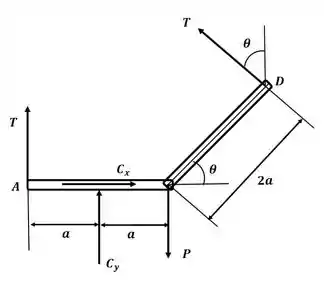
Ok! Agora, para descobrir o valor da tensão , vamos aplicar o somatório de momentos para o sistema com relação ao ponto C:
Isolando , substituindo o valor de , simplificando o termo que aparece em todos os termos e resolvendo, temos:
Passo 2
Agora podemos aplicar o somatório de forças na direção para encontrar o valor de :
Substituindo o valor de encontrado no passo 1, o valor de e resolvendo:
Passo 3
E, aplicando o somatório de forças na direção :
Substituindo o valor de encontrado no passo 1, o valor de e resolvendo:
Resposta
Exercícios de Livros Relacionados
Três barras de controle são fixadas a uma alavanca ABC e exercem forças sobre ela como mostrado na figura. ( a ) Substitua as três forças por um sistema força-binário em B. ( b ) Determine uma única f
Uma viga de 4 m de comprimento está carregada como mostra a figura. Determine a carga do Problema 3.101 que é equivalente a essa carga.
O manipulador deuma esmeriladora industrial em miniatura pesa 2,7 N e seu centro de gravidade está sobre o eixo y . O cabeçote do manipulador fica recuado no plano x z de modo que a linha BC forma um
Uma viga de 4 m de comprimento está sujeita a uma variedade de cargas, ( a ) Substitua cada carga por um sistema força-binário equivalente na extremidade A da viga. ( b ) Quais das cargas são equivale
105- Os pesos de duas crianças sentadas nas extremidades A e B de uma gangorra são 370N e 280N , respectivamente. Onde deverá sentar-se uma terceira criança de modo que a resultante dos pesos das três