Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 152

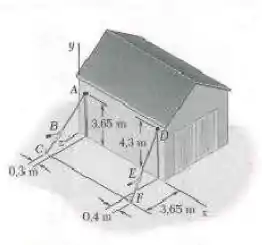
Resolva o Problema 3.151 quando a tensão no cabo A B é 1.360 N .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

A questão quer saber o valor de T_D E quando T_A B = 1 360 N . A primeira coisa que temos que fazer é o diagrama de corpo livre para poder relacionar essas tenções:

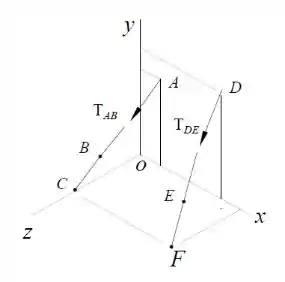
Observe que no enunciado, nos foi dito que o somatório dos momentos, exercidos pelas tensões T_A B e T_D E , em torno do eixo x seria igual a 6400 N * m .

Pelo diagrama, podemos notar que somente as componentes em z das forças geram momento em torno de x , portanto teremos o seguinte arranjo:

M_x = (T_A B)_z * y_A + (T_D E)_z * y_D

Passo 2

Agora que já temos uma relação entre as tensões, precisamos descobrir as incógnitas.

Sabemos que:

M_x = 6400 N * m

(T_A B)_z = T_A B cos theta_1

(T_D E)_z = T_D E cos theta_2

Precisamos então descobrir os ângulos que as tensões fazem com a vertical.

Vamos descobrir os comprimentos A C e D F . Temos que:

A C = A - C

A C = (0,3 i + 3,65 j + 0 k) - (0 i + 0 j + 3,65 k)

Resolvendo, temos:

A C = (0,3 i + 3 , 65 j - 3,65 k)

Seu módulo será:

|A C| = sqrt((0,3)^2 + (3 , 65)^2 + (- 3,65)^2)

|A C| = 5,17 m

Para D F , temos o mesmo procedimento:

D F = D - F

D F = (0 i + 4,3 j + 0 k) - (0 , 4 i + 0 j + 3,65 k)

Resolvendo, temos:

D F = (- 0,4 i + 4,3 j - 3,65 k)

Seu módulo será:

|D F| = sqrt((- 0 , 4)^2 + (4,3)^2 + (- 3,65)^2)

|D F| = 5 , 65 m

Passo 3

Agora ficou fácil de encontrar os ângulos:

cos theta_1 = (3,65)/(5,17)

cos theta_1 = 0,706

Resolvendo o cos theta_2 , temos:

cos theta_2 = (3,65)/(5,65)

theta_2 = 0,645

Portanto, substituindo os valores conhecidos, temos:

(T_A B)_z = (1 360) ( 0,706 )

(T_A B)_z = 960,16 N

(T_D E)_z = T_D E (0,645)

Passo 4

Utilizando a equação do momento, temos:

M_x = (T_A B)_z * y_A + (T_D E)_z * y_D

Substituindo os resultados, temos:

6400 = (960,16) (3,65) + (0,645 T_D E) (4,3)

Isolando T_D E e resolvendo, encontraremos:

T_D E = 1043,3 N

Resposta

T_D E = 1043,3 N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

46. Um poste de telefone de 6m com peso 1600N é usado para manter as extremidades de dois fios suspensas. Os fios formam com a horizontal os ângulos mostrados na figura, e as trações nos fios são, res
43. Uma massa de 8k g pode ser sustentado das três diferentes maneiras mostradas nas figuras. Sabendo que as polias têm um raio de 100m m , determine a reação em A em cada caso.
50. Determine o intervalo de valores admissíveis da tração no arame B D sabendo que a intensidade do binário no engaste C não pode exceder 100N ⋅ m
49. Determine a força nos membros HI, FI e EF da treliça e diga se os membros estão em tração ou compressão.
42. Resolva o Problema 4.41 se a corda B E é paralela às hastes ( α = 30 ° ) .