Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 110
O pino está submetido a cisalhamento duplo, visto que é usado para interligar os três elos. Devido ao desgaste, a carga é distribuída nas partes superior e inferior do pino como mostra o diagrama de corpo livre. Determine a carga máxima que o acoplamento pode suportar se a tensão de cisalhamento admissível para o material for e o diâmetro do pino for . Determine também as intensidades das cargas .
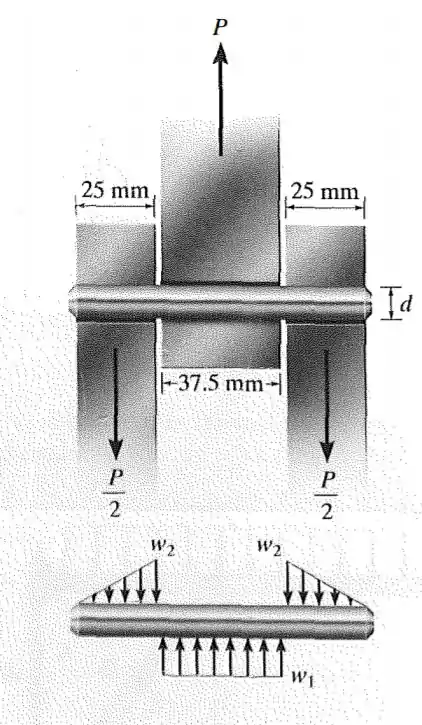
Passo 1
Desejamos encontrar os valores das cargas distribuídas e para isso vamos utilizar o somatório das forças no eixo para o pino e para os elos, esses sofrerão cisalhamento duplo e portanto a força será dividida por 2. Além disso, precisamos encontrar primeiramente o valor da carga e a obteremos aplicando a fórmula da tensão de cisalhamento média.
Passo 2
A partir da fórmula da tensão de cisalhamento média vamos obter
Onde
Dessa forma, vamos obter
Dessa forma, tomemos o somatório das forças no eixo para o pino e os elos e vamos obter