Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 182
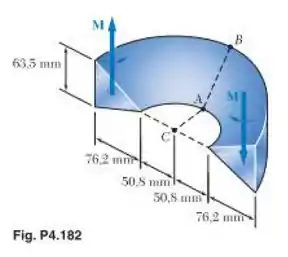
Sabendo que M = 565 N.m, determine a tensão no (a) ponto A e (b) ponto B.
Passo 1
Beleza! Vamos começar esse exercício escrevendo o raio interno da seção, que pode ser visto através da figura do enunciado como a distância do centroide C até a base do triângulo, então temos:
Agora, para o raio externo da seção, que será dado pelo raio interno mais a altura do triângulo, temos:
Agora vamos calcular a área da seção, então temos:
Agora vamos escrever o raio médio da seção, para isso, basta lembrar que o centroide do triângulo está a 1/3 da sua altura total com relação a base, então no nosso caso, basta somar 2/3 da altura ao comprimento do centroide até a base do triângulo, sendo assim, teremos:
Agora, para encontrar a localização do raio da superfície neutra da seção, vamos recorrer a fórmula para a seção trapezoidal apresentada na figura 4.61 dessa seção. Observe que não podemos usar a fórmula para a seção triangular, pois a fórmula apresentada foi desenvolvida orientando-se do centroide até a base do triângulo, e não do centroide ao vértice superior (como é o caso da seção apresentada). Dessa forma, vamos utilizar a fórmula para a seção trapezoidal, onde temos:
Só que, no nosso caso, como a seção em si é triangular, basta que adotemos . Então, substituindo os valores conhecidos, chegamos em:
Passo 2
Agora podemos encontrar a excentricidade da seção, que é a distância entre a linha neutra e o centroide da seção, através de:
Substituindo os valores conhecidos, teremos:
Agora para encontrar a tensão no ponto A pedida na letra (a), vamos utilizar a equação 4.71 vista nessa seção, onde temos:
No ponto A temos , então a equação acima se torna:
Substituindo os valores conhecidos, chegamos em:
Passo 3
Agora para encontrar a tensão no ponto B pedida na letra (b), nós vamos repetir o último cálculo do passo 2, só que agora com . Então a equação 4.71 se torna:
Substituindo os valores conhecidos, chegamos em: