Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 155b

Sabendo-se que a carga de 120   k N pode ser aplicada a qualquer ponto da circunferência de raio 40 m m mostrada, determinar:

  1. A correspondente tensão em A ,   B   e   D

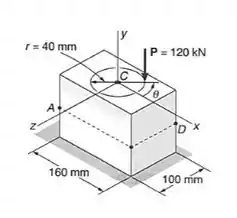
Passo 1

Para determinação de tensões em elementos que estão sujeitos a momentos fletores inclinados, ou ainda, momentos fletores oblíquos, ou momentos fletores assimétricos, temos a seguinte fórmula:

σ = - P A + M z x I z z - M x z I x x

Em que:

M z = p a r c e l a   d o   m o m e n t o   n a   d i r e ç ã o   z

M x = p a r c e l a   d o   m o m e n t o   n a   d i r e ç ã o   x

x   e   z = c o o r d e n a d a s   n o   p o n t o   e m   q u e   s e   d e s e j a   s a b e r   a   t e n s ã o   e m   c a d a   d i r e ç ã o

I z z = m o m e n t o   d e   i n é r c i a   e m   t o r n o   d e   z

I x x = m o m e n t o   d e   i n é r c i a   e m   t o r n o   d e   y

Primeiro temos que determinar os momentos em cada uma das direções, ou seja, vamos abrir os momentos fletores em cada uma das direções, e depois analisamos cada uma das direções, sendo assim teremos que:

Decompondo os momentos fletores teremos que:

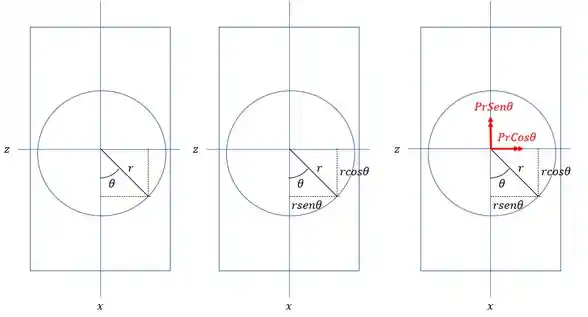
Sabemos que os momentos são dados por:

M z = - P r C o s θ

M x = - P r S e n θ

Agora que já temos os momentos fletores em cada direção, podemos analisar cada uma delas separadamente.

Passo 2

Se definirmos a seção dessa seguinte maneira:

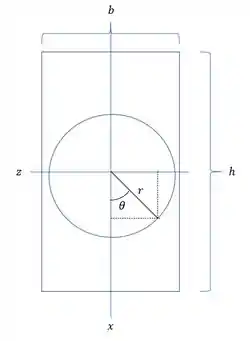
Teremos que:

A = b h

I x x = h b 3 12

I z z = b h 3 12

Como queremos a tensão em D, precisamos das coordenadas X e Z do ponto D, sendo assim teremos que:

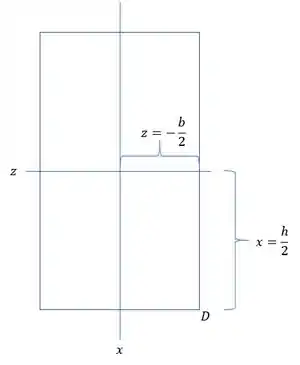
Substituindo nas tensões teremos que:

σ = - P A + M z x I z z - M x z I x x

σ = - P b h + - P r C o s θ   .   h 2 b h 3 12 - - P r S e n θ   .   - b 2 h b 3 12

σ = - P b h - 12 P r C o s θ   .   h 2 b h 3 - 12 P r S e n θ   . b 2 h b 3

σ = - P b h - 6 P r C o s θ b h 2 - 6 P r S e n θ h b 2

Como queremos a tensão máxima, vamos derivar em função do ângulo θ e vamos igualar a zero, sendo assim teremos que:

0 = 6 P r S e n θ b h 2 - 6 P r C o s θ h b 2

Com isso teremos que:

6 P r C o s θ h b 2 = 6 P r S e n θ b h 2

6 P r h b 2 b h 2 6 P r = S e n θ C o s θ = T g θ

T g θ = h b

Com isso temos que lembrar que:

h = 160   m m

b = 100   m m

Substituindo, teremos que:

T g θ = 160 100 = 160 100 = 1,6

θ = A r c T g   1,6 = 58 °

Ou ainda podemos fazer:

θ = 180 ° + 58 ° = 238 °

Passo 3

Como queremos a tensão que ocorre em em D, podemos substituir os dados que temos, sendo assim teremos que:

σ D = - P b h - 6 P r C o s θ b h 2 - 6 P r S e n θ h b 2

P = 120   k N = 120000   N

θ = 58 °

h = 160   m m

b = 100   m m

r = 40   m m

Substituindo teremos que:

σ D = - 120000 100   .     160 - 6   .   120000 .   40   .   C o s 58 ° 100   .     160 2 - 6   .   120000 .   40   .   S e n 58 ° 160   .     100 2 = - 28,7 N m m 2

σ D = - 28,7   M P a  

Para a tensão em A, precisamos das coordenadas, pois os outros valores nós já temos:

Substituindo nas tensões teremos que:

σ = - P A + M z x I z z - M x z I x x

σ A = - P b h + - P r C o s θ   . - h 2 b h 3 12 - - P r S e n θ   .   b 2 h b 3 12

σ A = - P b h + 12 P r C o s θ   . h 2 b h 3 + 12 P r S e n θ   . b 2 h b 3

σ A = - P b h + 6 P r C o s θ b h 2 + 6 P r S e n θ h b 2

Substituindo teremos que:

σ A = - 120000 100   .     160 + 6   .     120000   .     40   .     C o s 58 100   .     160 2 + 6   .     120000   .     40   .     S e n 58 160   .     100 2 = 13,7 N m m 2

σ A = 13,7 M P a

E por fim podemos determinar a tensão no ponto B

Substituindo nas tensões teremos que:

σ = - P A + M z x I z z - M x z I x x

σ B = - P b h + - P r C o s θ   . h 2 b h 3 12 - - P r S e n θ   . b 2 h b 3 12

σ B = - P b h - 12 P r C o s θ   . h 2 b h 3 + 12 P r S e n θ   . b 2 h b 3

σ B = - P b h - 6 P r C o s θ b h 2 + 6 P r S e n θ h b 2

Substituindo teremos que:

σ B = - 120000 100   .     160 - 6   .     120000   .     40   .     C o s 58 100   .     160 2 + 6   .     120000   .     40   .     S e n 58 160   .     100 2 = 1,803 N m m 2

σ B = 1,803   M P a

Resposta

  1. θ = 58 °   o u   θ = 238 °
  2. σ D = - 28,7   M P a       e     σ B = 1,803   M P a     e     σ A = 13,7 M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra curva mostrada tem a seção transversal de 30 x 30 mm. Sabendo que a tensão admissível na compressão é 175 MPa, determine a maior distância a admissível.
Para o anel aberto mostrado na figura, determine a tensão no (a) ponto A e (b) ponto B.
Sabendo que a máxima tensão admissível é 45 MPa, determine a intensidade do maior momento M que pode ser aplicado aos componentes mostrados.
Três chapas são soldadas umas às outras para formar a barra curva mostrada na figura. Para o carregamento dado, determine a distância e entre a linha neutra e o centroide da seção transversal.
Três chapas são soldadas umas às outras para formar a barra curva mostrada na figura. Para o carregamento dado, determine a distância e entre a linha neutra e o centroide da seção transversal.(Obs: pe