Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 37
Uma barra de poliestireno consiste de duas porções cilíndricas AB e BC, restringidas em ambas as extremidades, e suporta duas cargas de como indicado. Sabendo-se que determinar: (a) as reações em A e D; (b) a tensão normal em cada porção da barra.
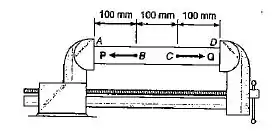
Passo 1
Fala aí galera, bora garantir aquele notão em Resmat? Para isso temos que resolver mais questões. Como o problema tem simetria, as reações serão exatamente iguais as forças aplicadas, mas em sentidos contrários. Logo:
Passo 2
Para determinar as tensões, temos que determinar os esforços atuantes em cada parte da barra. A área da barra será dada por:
De até temos uma força de atuando, logo:
Em , este esforço é cancelado pela força logo:
Já a partir de temos um esforço de compressão de portanto:
Resposta
Exercícios de Livros Relacionados
Num arame de alumínio de 4 m m de diâmetro, é observado um alongamento de 25 m m , quando a tração no arame é de 400 N . Sabendo-se que E = 70 G P a e, que a tensão última para o alumínio é de 110M P
Uma barra de alumínio de 1,5 m de comprimento não poderá alongar-se mais do que 1 m m e a tensão normal não exceder a 40M P a , quando estiver sujeito a uma carga axial de 3 k N . Sabendo-se que E = 7
Resolver o P r o b .2.5 7 , considerando que a porção AB da barra composta é de aço e a porção BC de latão.
Um arame de aço de 60 m de comprimento não deve alongar-se mais do que 48 m m , quando é aplicado uma tração de 6 k N . SendoE = 200G P a , determinar:O menor diâmetro que pode ser especificado para o
Um arame de 80 m de comprimento e diâmetro de 5 m m é feito de um aço com E = 200G P a e tensão última de 400M P a . Se um coeficiente de segurança de 3,2 é desejado, qual é:A maior tração admissível