Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 96
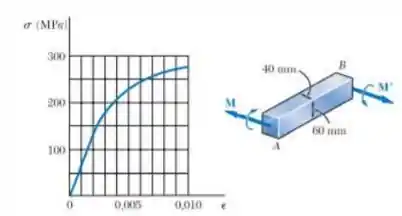
A barra prismática é constituída de uma liga de alumínio para a qual a curva de tensão-deformação específica em tração é mostrada na figura considerando que a curva de em função de é a mesma em compressão e em tração, determine,
- O raio de curvatura da barra quando a tensão máxima é de e.
- O valor correspondente do momento fletor. (sugestão: para a parte , construa uma curva de em função de e use um método aproximado de integração.)
Passo 1
O item a) é o mais tranquilo de todos, então vamos garantir ele, e depois vamos para o item b) que vamos ter um pouquinho mais de trabalho, mas nada muito absurdo.
Perceba que temos um diagrama que relaciona tensão com deformação especifica, e também temos uma equação que relaciona deformação especifica com o nosso raio de curvatura, e essa equação é dada por:
O é muito fácil, é metade da altura da nossa seção, ou seja, temos que:
O valor de nós iremos tirar da nossa tabela, porque pensa só, sabemos que queremos o raio de curvatura para o caso de tensão sendo igual a , sendo assim, teremos que:
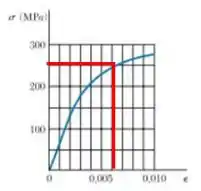
Substituindo na nossa equação, teremos que:
Passo 2
Para o item b) queremos determinar os nossos momentos fletores, e relacionando o nosso momento com a nossa integral, teremos que:
Em que é metade da altura da seção e é a largura da nossa seção. Quando temos seções retangulares, podemos fazer a seguinte simplificação:
Podemos definir que:
Se definimos que
Temos que:
Podemos definir que:
Derivando dos dois lados temos que:
Substituindo teremos que (lembrar que para a variação era de até , como estamos mudando para , a variação vai passar a ser de 0 até 1:
Se definimos que:
Podemos fazer uma aproximação numérica para o método de integração, e para isso temos que tomar um certo cuidado, para o método numérico obteremos a seguinte equação:
E para isso faremos as seguintes premissas de cálculo:
- O valor de varia entre 0 e 1 e faremos isso em intervalos de
- Os valores de são utilizados no seguinte sentido:
- Para as extremidades w=1
- Para as posições impares w=4
- Para as posições pares w=2
Sabido isso, podemos montar a nossa seguinte tabela de cálculo.
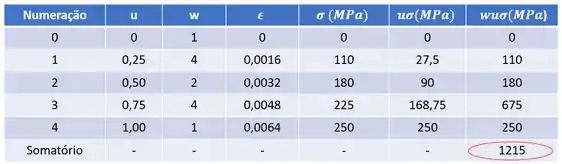
Assim temos que:
Substituindo na nossa equação principal, teremos que: