Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 74

Uma viga com a seção transversal mostrada na figura é constituída de um aço elastoplástico, com E = 200 G P a e σ e = 240   M P a . Para flexão em torno do eixo z, determine o momento fletor no qual.

  1. Inicia-se o escoamento
  2. As zonas plásticas nas partes superior e inferior da barra têm 30mm de espessura.

Passo 1

Sabemos que a equação de tensão é dada por:

σ = M y I

Como queremos o momento que começa a gerar o escoamento da seção, podemos fazer a seguinte igualdade:

σ E = M y I

Como queremos o momento fletor, precisamos fazer o seguinte:

M = σ E I y

Assim a nossa seção é dada por:

Assim temos que:

I = 2 I 1 + I 2 = 2 × 15 × 30 3 12 + 30 × 90 3 12 = 1890000   m m 4

y + = 45   m m

σ E = 240   M P a = 240 N m m 2

M = 240 N m m 2 1890000   m m 4 45   [ m m ]

M = 10080000   N m m

M = 10,08   k N m

Passo 2

Sabemos pelo enunciado que os 30 m m superiores e inferiores são a região plástica, significa que a tensão máxima que ela chega é a de escoamento, e entre as duas regiões de 30 mm existe a região plástica, e na região plástica, o funcionamento das tensões funciona da maneira que já sabemos, ou seja, vai reduzindo até chegar a zero na L N , assim tem-se que:

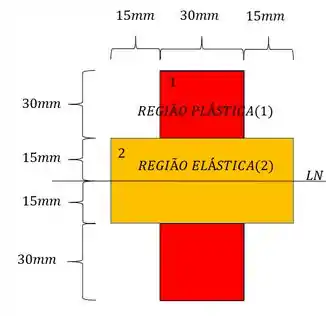
E o diagrama de tensões é dado por: (Vale lembrar que na região plástica máxima é a de escoamento, que fica constante até o ponto da região plástica)

F 1 = A 1 σ E = 30 m m × 30 m m × 240 N m m 2 = 216000   N

F 2 = A 2 σ E = 15 m m × 60 m m × 240 2 N m m 2 = 108000   N

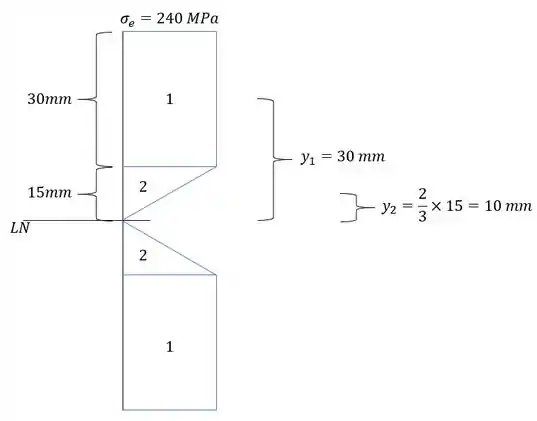
Como temos seções acima e embaixo, temos que multiplicar por 2, assim, o nosso momento vai ser dado por:

M = 2 ( F 1 y 1 + F 2 y 2 )

M = 2 ( 21600 0 N × 30 [ m m ] + 108000 N × 10 [ m m ] )

M = 7560000   N m m

M = 7,56   k N m

Resposta

  1. M = 10,08   k N m

  2. M = 7,56   k N m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O diagrama tensão–deformação para uma liga de titânio pode ser aproximado pelas duas retas mostradas na figura. Se uma escora feita desse material for submetida a flexão, determine o momento ao qual e
A viga é feita de um material elástico plástico para o qual σe = 200 MPa. Se o maior momento na viga ocorre no interior da seção central a-a, determine o valor de cada força P que faz com que esse mom
A barra de plexiglass tem uma curva tensão – deformação que pode ser aproximada pelos segmentos de reta mostrados na figura. Determine o maior momento M que pode ser aplicado à barra antes que ela fal
O elemento é feito de material elástico perfeitamente plástico para o qual σe = 230 MPa. Determine o momento elástico máximo e o momento plástico que podem ser aplicados à seção transversal. Considere
A viga é feita de um material fenólico, um plástico estrutural, cuja curva tensão deformação é mostrada na figura. Se uma porção da curva puder ser representada pela equação σ = [5(106)ε]1/2 MPa, dete