Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 68
Resolva o , considerando que o momento fletor é paralelo ao eixo .
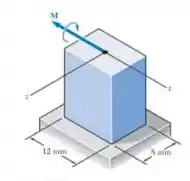
Passo 1
Sabemos que a equação de tensão é dada por:
Como queremos o momento que começa a gerar o escoamento da seção, podemos fazer a seguinte igualdade:
Como queremos o momento fletor, precisamos fazer o seguinte:
Assim a nossa seção é dada por:
Assim temos que:
Passo 2
A fórmula que precisamos usar para o caso de núcleos elásticos com momentos agindo, precisamos usar a seguinte equação:
Com isso sabemos que:
E esse já determinamos no caso anterior, assim, temos que:
Pela seção temos que:
E agora só precisamos determinar
Como o nosso núcleo elástico possui de espessura, podemos escrever ele como:
Substituindo isso na nossa equação teremos que:
Resposta
Exercícios de Livros Relacionados
A barra curva usada em uma máquina tem seção transversal retangular. Se a barra for submetida a um conjugado, como mostra a figura, determine as tensões de tração e compressão máximas que agem na seçã
Uma barra curva é usada em uma máquina e tem seção transversal retangular. Se a barra estiver sujeita a um conjugado, como mostra a figura, determine as tensões de tração e compressão máximas que agem
A viga é feita de um material que pode ser considerado como perfeitamente plástico sob tração e plástico sob compressão. Determine o momento fletor máximo M que pode ser suportado pela viga de modo qu
Determine o momento plástico Mp que pode ser suportado por uma viga que tenha a seção transversal mostrada na figura σe = 210 MPa.
Determine o módulo da seção plástica e o fator de forma para o elemento que tem seção transversal tubular