Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 105
Para a barra do Prob. 4.104, determinar: (a) o raio de curvatura da barra, quando a tensão máxima é 310 MPa; (b) o correspondente valor do momento fletor. (Veja a sugestão dada no prob. 4.102).
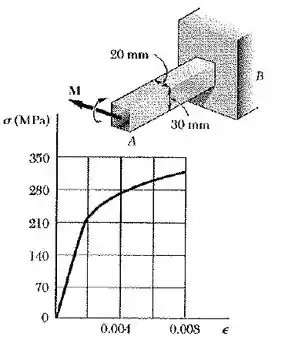
Passo 1
Inicialmente do enunciado nós temos
Com isso podemos verificar o gráfico e encontrar o valor de
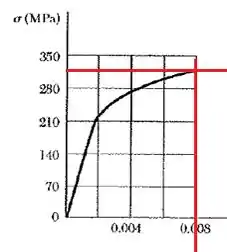
Observa que tracei uma reta em , e no gráfico encontramos um valor muuuito próximo de 0,008 para . Então
Para o c teremos
Como a altura de nossa barra é de 30mm
O valor de b nos foi passado que éa espessura da barra
Com isso temos então, para encontrarmos o raio de curvatura:
Passo 2
O cálculo do momento fletor pode ser meio chatinho, mas uma vez que você entende o passo a passo, já era. Primeiramente temos a relação
Vamos chamar de simplesmente por ser comum encontramos assim nos livros didáticos.
Temos então para o momento
Lembre-se que fiz essa substituição final por que nos é dado por .
Passo 3
Usando a regra de Simpson, a fórmula da integral fica
Onde w é o carregamento. Usando encontramos alguns valores que tabelei abaixo.
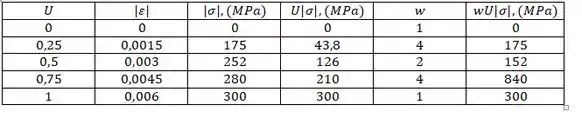
O somatório dos valores de na tabela nos dá
Então o calculo de fica
Então pra fechar a questão e encontrarmos M