Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 115
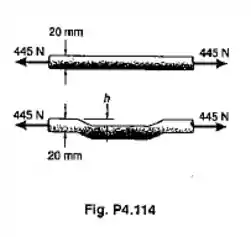
Resolva o Prob. 4,114, considerando que a barra é substituída por um tupo de 20 mm de diâmetro externo e 16 mm de diâmetro interno.
Passo 1
Bom, para a teremos
Onde a área será dada pela diferenã da área com diâmetro externo e interno
O enunciado nos diz que a tensão máxima não deve passar de 3 vezes a tensão da barra, logo (respondendo já a letra b, haha)
Para o somatório do momento teremos
E por último a inércia da circunferência
Passo 2
A letra a nos pergunta quanto vale h, para isso faremos
Isolando o h encontramos
Resposta
Exercícios de Livros Relacionados
Uma viga com a seção transversal mostrada na figura é submetida a um momento M 0 atuando em um plano vertical. Determine o maior valor admissível do momento M 0 para que a tensão máxima não ultrapasse
Para o elemento de máquina e a carga mostrados, determine a tensão nos pontos A e B quando h = 2,5 in.
Para o elemento de máquina e a carga mostrados, determine a tensão no ponto A quando (a) h = 2 in., (b) h = 2,6 in.
Para a barra curva mostrada na figura, determine a tensão nos pontos A e B quando h = 55 mm.
Para a barra curva mostrada na figura, determine a tensão no ponto A quando (a) h = 50 mm e (b) h = 60 mm.