Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 106

Uma barra prismática de seção transversal retangular é feita por uma liga para a qual a curva tensão-deformação específica pode ser representada pela relação ϵ = k σ n , para σ > 0 e ϵ = - k σ n para σ < 0 .   Se um momento fletor M é aplicado à barra, mostre que a tensão máxima é

σ m = 1 + 2 n 3 n M c I

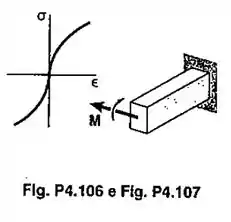
Passo 1

Primeiramente temos a relação

ε = - ε m y c

Vamos chamar y c de U simplesmente por ser comum encontramos assim nos livros didáticos.

Temos então para o momento

M = - ∫ - c c y σ b   d y = 2 b ∫ 0 c y σ   d y = 2 b c 2 ∫ 0 1 U σ   d U

Para ε = K σ n ,   ε M = K σ

ε ε m = U = σ σ m n

σ = σ m U 1 n

Passo 2

Então nosso M fica

M = 2 b c 2 ∫ 0 1 U σ   d U = 2 b c 2 σ m ∫ 0 1 U 1 + 1 n   d U

= 2 b c 2 σ m U 2 + 1 n 2 + 1 n   | 1 0  

= 2 n 2 n + 1 b c 2 σ m

σ m = 2 n + 1 2 M b c 2  

Passo 3

Lembrando que

I c = b 2 c 3 12 c = 2 3 b c 2

1 b c 2 = 2 c 3 I

σ m = 2 n + 1 3 n M c I

Resposta

σ m = 2 n + 1 3 n M c I

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolver o P r o b .4.118 , considerando que a tensão admissível compreensiva é reduzida para 60M p a .
Sabendo-se que o grampo mostrado foi apertado até produzir P = 400N , determinar:A tensão no ponto AA tensão no ponto BA posição da linha neutra na seção a-a
Resolver o P r o b .4.120 , considerando que o raio de cada um dos semi-círculos da seção transversal do grampo é aumentada de 2 m mp a r a3 m m .
A um bloco de madeira de 100m mx100m m de seção transversal, são pregadas quatro pranchas de seção transversal 25 m mx100m m . Pede-se:Determinar a tensão compressiva no bloco, causada por uma carga a
Uma fresadora foi usada para remover uma porção de uma barra, ao longo de seu eixo. Sabendo-se que o diâmetro da barra é 20 m m , e que forças de 4 k N atuam nos centros das extremidades da barra, det