Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 45
Uma barra rígida é sustentada, como indicado, por dois arames de aço de de diâmetro (), um pino e um suporte em . Sabendo-se que os arames estão incialmente esticados, determinar: (a) a tração adicional em cada arame, quando uma força de é aplicada em ; (b) a correspondente deflexão no ponto .
Passo 1
O problema pede a tração em cada arame e a deflexão do ponto . Ou seja, vamos ter que utilizar, tanto uma equação de forças, no caso o equilíbrio das forças na vertical e o momento, quanto a equação da deflexão.
Vamos aplicar o momento em porque é onde as forças, além de desconhecidas, não nos interessam.
Passo 2
Vamos fazer o diagrama de corpo livre da barra
Agora vamos aplicar as equações de equilíbrio:
Podemos simplificar tudo por 200
Perceba que nós temos duas equações e três incógnitas, e na verdade nem precisamos descobrir então a única equação que vai realmente importar nesse caso é a segunda.
Então para descobrir as forças e vamos ter que utilizar a equação da deflexão.
Passo 3
A deflexão que vamos utilizar, neste caso, será dos fios, da seguinte forma:
Substituindo os valores vamos achar:
Com , e a área é dada por
Para o arame :
Com , e a área é dada por
Tá, mas e aí? Essas equações ainda significam BULHAFAS!
Agora vamos utilizar a nossa boa e velha GEOMETRIA!
Passo 4
Se a força está para baixo é evidente que a barra irá girar para baixo, então vamos desenhar como vai ficar a nova posição de equilíbrio da barra.
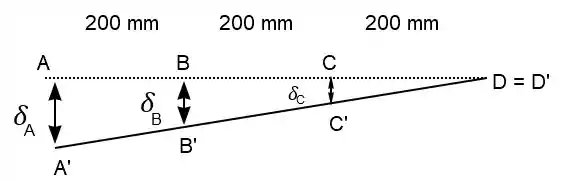
Onde representam os pontos originais da barra e representam os pontos da barra após a aplicação da força .
A gente já calculou e em função das forças e agora podemos, por meio de uma semelhança de triângulos, achar uma relação entre as próprias deflexões.
Os triângulos , e são todos semelhantes, por isso podemos escrever:
Como queremos uma relação entre e :
Simplificando por 200
Multiplicando cruzado
Passo 5
Agora voltamos a relação das forças em conjunto com a relação de deflexões que acabamos de achar.
Vale lembrar que o deslocamento do fio é igual ao do ponto em questão.
Assim:
Assim, podemos substituir as duas últimas equações na terceira:
Reorganizando
Basta substituir na primeira equação
E
Fechamos a letra A.
Passo 6
Agora para fazermos a letra B vamos voltar para a geometria:
Como já sabemos as forças, podemos facilmente achar as deflexões:
Assim, podemos pegar qualquer uma dessas relações e substituir na da geometria:
Simplificando por 200
Multiplicando cruzado:
Resposta
a)
b)