Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 1.Problemas - Ex. 20
Para a treliça e carregamento mostrado, determine a tensão normal na barra . Sabe-se que a área da seção transversal da barra é de .
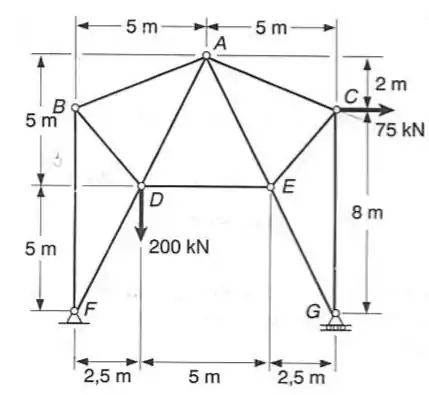
Passo 1
O problema a pede a menor tensão normal, que pode ser calculada a partir da área da seção transversal () e da força atuante na barra. Aqui a dificuldade deste problema se encontra em achar a força atuante na barra . Então vamos fazer isso pelo métodos dos nós.
A sequência que iremos fazer será a seguinte:
- Achar as tensões de e
- Analisar o nó para achar a tensão
- Analsar o nó para achar a tensão .
- Método das seções cortando a barra .
Passo 2
Vamos achar as tensões e
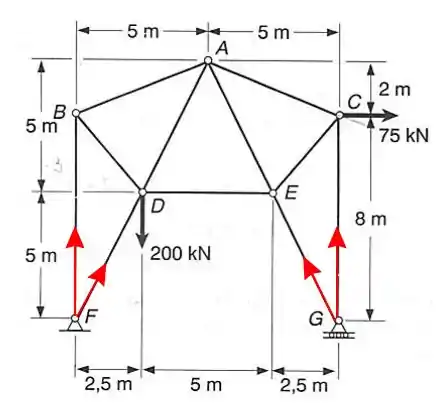
Como o apoio do ponto é um apoio que permite deslocamento no eixo então não pode haver forças neste eixo, portanto a tensão em é igual a zero.
A partir daí podemos aplicar o momento em relação ao ponto e vamos ter:
Passo 3
Analisar o nó
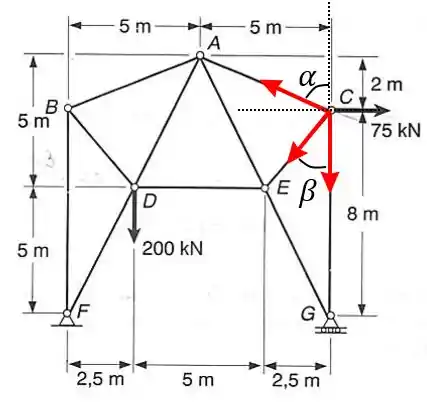
Para fazer a análise corretamente temos de descobri os ângulos e
Agora podemos aplicar o somatório das forças em e em
Resolvendo as equações:
Vamos dividir a primeira equação por 0,77 e multiplicar por 0,64 em seguida:
Somando com a segunda
obtemos:
Substituindo na equação para achar
Passo 4
Agora vamos analisar o nó
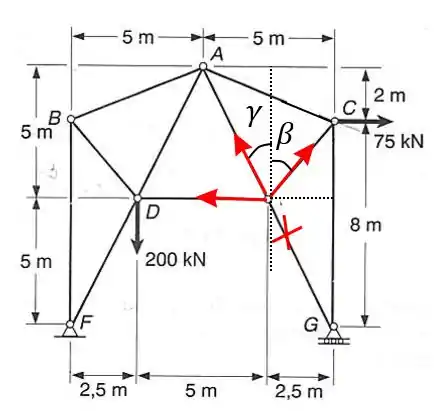
Como já vimos a tensão em é igual a zero, portanto foi desconsiderada.
Agora temos que achar o ângulo que será:
Agora podemos aplicar as equações de equilíbrio:
Passo 5
Vamos aplicar o método das seções:
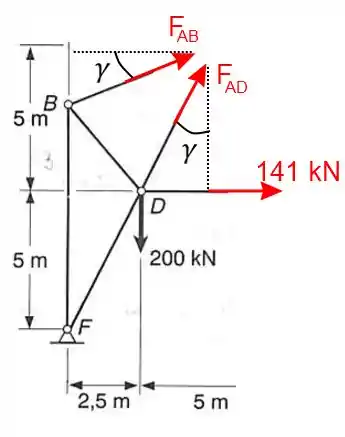
Agora, aplicando as equações de equilíbrio:
Passo 6
Agora basta aplicar a equação da tensão: