A barra rígida é sustentada por um pino em e dois cabos de aço, cada um com diâmetro de . Se a tensão de escoamento para os cabos for e , determine a intensidade da carga distribuída que pode ser colocada sobre a viga e provocará um início de escoamento no cabo . Qual é o deslocamento do ponto para se caso? Para o cálculo, considere que o aço é elástico perfeitamente plástico.

Estamos procurando forças, então primeiro vamos ver no diagrama de corpo livre como elas se relacionam. O que nos interessa são as forças verticais.

A situação que estamos buscando é quando o cabo começa a escoar, o que significa que a tensão no cabo é

Pela fórmula da tensão, , podemos calcular já de cara qual é a força que o cabo está suportando:

Show, já é uma informação resolvida! Vamos ver o que isso tem a ver com , que é quem procuramos.

Fazendo equilíbrio de momentos em a gente não tem que lidar com a reação do pino. Atenção que o carregamento atua a de com itensidade de .

Hmmm, pra definirmos ainda precisamos descobrir o que está acontecendo com a força . Vamos ver a compatibilidade.

A barra vai girar ao redor do pino em . Como ela é rígida, ela não se deforma. Vejamos como os deslocamentos dos cabos se relacionam. A barra é a linha preta na figura.

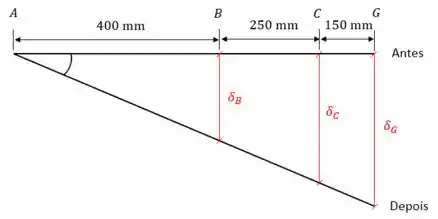
Na figura temos três triângulos com um ângulo em comum. Olhando para o menor e o intermediário, podemos formar uma equação com a tangente do ângulo:

Antes de fazer um monte de conta, pense o seguinte:

• O cabo começou a escoar agora quando ele esticou .
• O cabo é igual ao cabo (mesmo material e mesmo comprimento inicial!).
• Se , então obviamente o cabo já deformou mais que o cabo !
• Então o cabo já está em regime plástico!!

Percebendo isso a gente evita muita conta que seria só pra checar que não está no regime elástico. O cabo sempre escoa antes do cabo

Vamos ver como é no regime plástico para finalmente acharmos .

O cabo já está em deformação plástica há um tempo, mas como ele é feito de material elastoplástico a tensão nele continua sendo

Então pela fórmula da tensão, a força também vai ser

Agora que temos as forças nos cabos, podemos definir pelo equilíbrio de momentos:

Show. Vamos ver como ficou para fechar essa questão.

Volte na figura do Passo 3. Olhando para o menor e o maior triângulo, podemos formar uma equação com a tangente do ângulo:

Ah, mas a gente tem como achar fácil! O cabo começou a escoar agora, então a deformação dele pode ser encontrada pela Lei de Hooke com a tensão :

Definição de deformação:

Então finalmente temos :