Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 99
A barra tem área de seção transversal de . Se uma força for aplicada em e, então, removida, determine a tensão residual nas seções e . .
Passo 1
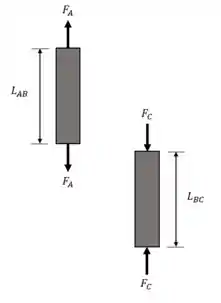
Uma barra vertical presa por pinos em e sofre um carregamento para baixo em .
Características da barra:
- Tensão de escoamento:.
- Área transversal: .
- Comprimentos iniciais: , . (Trate como conhecido!)
A carga é aplicada e então removida. Queremos saber qual é a tensão residual nas seções.
Bem, de início, a gente trata como se fosse um problema comum, estaticamente indeterminado. Primeiro vamos achar as tensões em cada seção da barra e ver se ultrapassam o limite de escoamento.
Passo 2
Problema com uma dimensão só, tá fácil! Os apoios vão resistir com e apontando pra cima:
Duas incógnitas ( e ), precisamos de mais uma relação. Vamos ver a compatibilidade.
Passo 3
Vamos pensar com o princípio da superposição. Olhe para o ponto .
- O carregamento puxa a seção para baixo, descendo um comprimento .
- A reação empurra a barra toda ( para cima, então sobe
Como o apoio é rígido em (não se move), esses efeitos tem que se anular:
Como estamos pensando no regime elástico ainda, então temos fórmula! Relação carga-deslocamento:
Opa! Bota os valores que a gente já acha uma reação:
Agora volta em que aí pegamos logo:
Passo 4
Agora que temos as reações, vamos conferir as tensões com a fórmula:
Os sinais nas tensões vão ser importantes mais tarde! Então entenda o que está acontecendo: a seção está sendo tracionada (positivo) e a seção está sendo comprimida (negativo).
Compare com para ver se alguma parte escoou.
Seção : . OK!
Seção : . Iiiiih, então essa seção não está no regime elástico...
Vamos ter que analisar de novo. A informação que temos agora é a seguinte: a seção com certeza vai escoar.
Passo 5
A questão devia ter nos dado alguma informação sobre a relação tensão-deformação no regime plástico (afff...). Como não disse nada, vamos supor que o material é elastoplástico. Então a tensão em vai continuar sendo , e aí a gente multiplica pela área pra ver qual é o máximo de força que essa parte da barra aguenta:
Beleza, agora vamos ver como fica . Use o equilíbrio de forças
Temos as reações! Mas calma, tem que conferir se nesse novo equilíbrio a seção continua em regime elástico:
Ótimo, a tensão está menor que o limite de escoamento ()! Se fosse maior, ia dar xabu (a barra ia deformar sem parar!)
Isso é tudo que tem pra gente descobrir a respeito da barra estar carregada:
- : regime elástico, tração, .
- : regime plástico, compressão, .
Agora vamos ver como resolve quando tiramos a força . Relaxa que é tranquilo!
Passo 6
Quando a força for retirada, ocorrerá um pouco de recuperação elástica da barra (mesmo em quem sofre deformação permanente; ). Porém, os apoios irão resistir essa recuperação, e teremos tensões residuais como resultado disso tudo.
O jeito fácil é pensar com o princípio da superposição: imagine uma força contrária ao carregamento, ou seja, empurrando para cima! Como a recuperação é elástica, as tensões induzidas vão ser aquelas calculadas no Passo 4!
Na seção , temos tração (positivo) de e recuperação (compressão, negativo) de . A tensão residual fica:
Na seção , temos compressão (negativo) de e recuperação (tração, positivo) de . Residual:
Ótimo! As duas deram iguais, como esperado. Fique atento que os sinais tem que ser iguais também nas tensões residuais!
Resposta
Tensão residual: (tração).