Determine o alongamento da barra no Problema quando são removidos tanto a carga quanto os apoios.

Antes de sair fazendo conta, vamos pensar um pouco: já dá pra descobrir qual seção escoa primeiro?

Bem, a ação da força vai deslocar algum comprimento para esquerda. Isso vai deformar as seções, comprimindo e esticando o mesmo comprimento! A definição de deformação é pegarmos justamente esse deslocamento e dividirmos pelo tamanho inicial:

Aí que vem a sacada! Perceba que ! Como é o mesmo , temos que sempre

Show! Então a seção sempre escoa primeiro, porque ela chega na deformação antes!

Por causa dessa sacada, a gente não precisa conferir nada de regime elástico! Quando entrar no regime plástico, a seção já vai ter escoado!

Agora vamos ver como ficam as forças com a barra inteira em regime plástico!

Beleza, então depois desse blá blá blá todo, vamos pras contas!

Estamos procurando uma força (), então vamos ver como está o equilíbrio. Só tem uma direção, as reações e vão resistir o carregamento.

Queremos o valor de quando a seção começa a escoar. Então a reação que está tracionando tem que gerar uma tensão

Pela fórmula da tensão, já podemos achar

Como vimos no Passo 2, quando escoar, a seção já vai estar em regime plástico. O material é elastoplástico, então a tensão se mantém sendo

De novo, pela fórmula da tensão:

Já matamos a primeira parte da questão!

Isso é tudo que nos interessa a respeito da barra estar carregada:

• : regime plástico, compressão, .
• : regime plástico, tração, .

Agora bora ver o que acontece quando tiramos o carregamento e os suportes!

Vamos com calma para não se perder! Podemos tratar a questão primeiro tirando só o carregamento e depois tirando os suportes! Princípio da superposição é uma beleza!

Quando a força for retirada, ocorrerá um pouco de recuperação elástica da barra. Porém, os apoios irão resistir essa recuperação, e teremos tensões residuais como resultado disso tudo.

O jeito fácil é pensar com o princípio da superposição: imagine uma força contrária ao carregamento, ou seja, empurrando para direita em ! A recuperação é elástica, então precisamos resolver o problema no regime elástico para descobrir quais forças são induzidas.

Vamos marcar como essas forças da recuperação. Vejamos a compatibilidade dos deslocamentos.

Para não se confundir, veja na figura como ficam as forças internas na recuperação elástica.

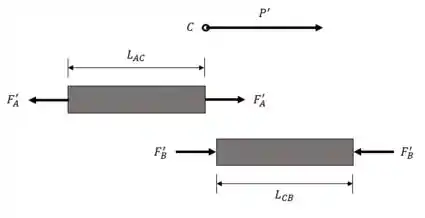
De novo, vamos com o princípio da superposição. Olhe para o ponto .

• O carregamento puxa a seção para direita, movendo para direita um comprimento .
• A reação empurra a barra toda ( para esquerda, então vai para a esquerda um comprimento

Como o apoio é rígido em (não se move), esses efeitos tem que se anular:

Estamos tratando de regime elástico. Relação carga-deslocamento

Beleza, vamos resumir o que ocorreu com a seção . A seção foi esticada (positivo) com quando tínhamos carregamento , e depois foi comprimida (negativo) quando tiramos o carregamento (efeito de . A força que sobra é

Essa é a força responsável pela tensão residual na barra depois que tirarmos ! Não precisamos calcular nada de nem nada disso, porque quanto não tem mais carregamento, a força em tem que ser a mesma que em (equilíbrio!).

Agora é muito simples! Essa força está comprimindo a barra, se tirarmos ela, é óbvio que a barra vai alongar. E o comportamento é elástico para (só é plástico a partir de ).