Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 70
A barra de seção vazada de parede fina tem uma seção transversal não circular com espessura de parede não uniforme. Usando a expressão dada na equação da seção e a expressão para a desnidade de energia de deformaçãp dada na equação , mostre que o ângulo de torção do elemento é
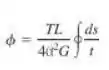
Em que é o comprimento da linha de esqueleto da seção transversal e é a área limitada por aquela linha de esqueleto.
Passo 1
Fala aí, galera. Tudo bem? Bora pra outra questão.
Primeiramente, da equação
A densidade de energia é dada por:
Substituindo:
Portanto:
Portanto, o ângulo de toruqe será:
Resposta
Exercícios de Livros Relacionados
Cada uma das barras de treliça mostrada é feita de aço e tem a seção transversal com as áreas indicadas. Usando E = 200G P a , determinar a energia de deformação da treliça para o carregamento mostrad
Na treliça mostrada, todos os membros são feitos do mesmo material e têm seções transversais uniformes, com as áreas indicadas. Determinar a energia de deformação da treliça, quando a carga P é aplica
Levando em conta somente o efeito das tensões normais, determinar a energia de deformação da viga prismática A B para o carregamento mostrado.
Assumindo que a viga prismática A B tem uma seção transversal retangular, mostrar que, para o carregamento dado, o máximo valor da densidade de energia de deformação na viga é u m = 15 U V onde U é a
Levando em conta somente o efeito das tensões normais, determinar a energia de deformação da viga prismática A B para o carregamento mostrado.