Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 17
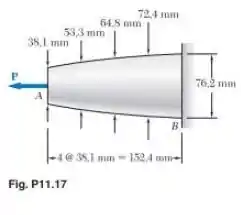
Usando determine de forma aproximada a máxima energia de deformação que a barra de alumínio acumulará se a tensão normal admissóivel é
Passo 1
Fala aí, galera. Tudo bem? Bora pra outra questão.
Primeiro, sabemos que a área da barra é:
A tensão admissível é Como tensão é força sobre área, podemos determinar a força. Logo:
A integral é dada por:
Resolvendo a integral:
Aqui, vou aplicar a regra de Simpson para resolver a integral, mas use o método que quiser. Logo:
Substituindo:
Resposta
Exercícios de Livros Relacionados
Um cilindro vazado de borracha liga uma barra A , de raio R 1 , a um tubo B , de raio interno R 2 , formando um suporte isolante de vibração. Denotando por G o módulo de elasticidade transversal da bo
Determinar a energia de deformação da barra prismática A B , levando em conta os efeitos das tensões normais e das tensões cisalhantes.
O estado de tensões mostrado ocorre em um componente de máquina, que é feito de um latão para o qual σ e = 175M P a . Usando o critério da máxima energia de distorção, determinar se o escoamento ocorr
O estado de tensões mostrado ocorre em um componente de máquina, que é feito de um latão para o qual σ e = 175M P a . Usando o critério da máxima energia de distorção, determinar a variação dos valore
O estado de tensões mostrado ocorre em um componente de máquina, que é feito de um aço para o qual σ e = 415M P a . Usando o critério da máxima energia de distorção, determinar o coeficiente de segura