Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 74

Cada elemento da treliça mostrada é feito de aço. A área da seção transversal do elemento B C   é de 800   m m 2 ,   e para todos os outros elementos a área é de 400   m m 2 .   Utilizando E = 200   G P a ,   determine a deflexão do ponto D   causada por uma carga de 60   k N .

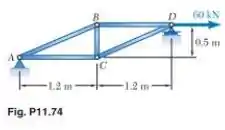
Passo 1

Fala aí, galera. Tudo bem? Bora pra outra questão.

Primeiramente, aplicando as equações de equilíbrio na peça inteira:

∑ M A = 0

2,4 R D = - 0,5 × 60 = 0

R D = 12,5   k N

Pegando o nó D :

∑ F y = 0

12,5 - 0,5 1,3 F C D = 0

F C D = 32,5   k N

∑ F x = 0

60 - F B D - 1,2 1,3 F C D = 0

F B D = 30   k N

Já no nó B :

∑ F x = 0

30 - 1,2 1,3 F A B = 0

F A B = 32,5   k N

∑ F y = 0

- 0,5 1,3 F A B + F B C = 0

F B C = 12,5   k N

Por fim, no nó C :

∑ F x = 0

- F A C + 1,2 1,3 32,5 = 0

F A C = 30   k N

Passo 2

Agora, a energia de deformação será calculada por:

U = ∑ F 2 L 2 E A = 1 2 E ∑ F 2 L A

Portanto, substituindo os valores nos trechos (barras):

U = 12,36 2 200 × 10 9 = 39,908   J

A deflexão em D   será:

1 2 P δ D = U

δ D = 2 U P = 1,03   m m

Prontinho!

Resposta

δ D = 1,03   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando E = 200G P a , determinar a energia de deformação devido à flexão, para a viga com o carregamento mostrado (desprezar o efeito das tensões de cisalhamento).
Usando E = 200G P a , determinar a energia de deformação devido à flexão, para a viga com o carregamento mostrado (desprezar o efeito das tensões de cisalhamento).
Usando E = 200G P a , determinar a energia de deformação devido à flexão, para a viga com o carregamento mostrado (desprezar o efeito das tensões de cisalhamento).
Usando E = 200G P a , determinar a energia de deformação devido à flexão, para a viga com o carregamento mostrado (desprezar o efeito das tensões de cisalhamento).
Dois eixos maciços são conectados pelas duas engrenagens mostradas. Usando G = 77G P a , determinar a energia de deformação em cada um dos eixos, quando um torque T de 1130N × m é aplicado em D .