Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 22
Para a barra e o suporte do Prob 2.18, determinar a maior carga P admissível, se a deflexão nos pontos A e B não devem exceder a e , respectivamente.
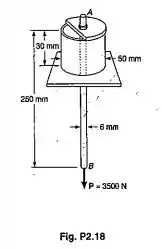
Passo 1
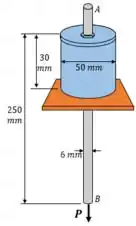
A melhor forma de começar essa questão é calculando as propriedades geométricas que vamos utilizar.
A área de seção transversal da barra:
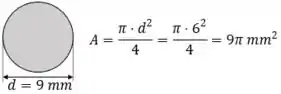
E calculamos o diâmetro interno do cilindro e depois sua área de seção transversal:
Passo 2
Primeiro vamos testar a deformação do ponto A. O deslocamento deste ponto é exatamente igual ao deslocamento da barra. Então podemos aplicar:
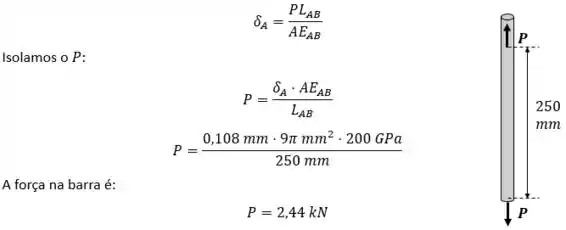
Passo 3
A deformação do ponto B será:
Resposta
A força admissível é a menor força calculada:
Exercícios de Livros Relacionados
Para a treliça de aço E = 200 G P a e carregamento mostrado, determinar as deformações nos membros B D e D E , sabendo-se que suas seções transversais tem 1300 m m 2 e 1950 m m 2
Um tubo cilíndrico de poliestireno de parede fina E = 3,1G P a , com 3,2m m de espessura e uma placa rígida circular (é ostrada apenas parte dela), são usadas para suportar uma barra de aço A B ( E =
Um tubo cilíndrico de poliestireno de parede fina E = 3,1G P a , com 3,2m m de espessura e uma placa rígida circular (é ostrada apenas parte dela), são usadas para suportar uma barra de aço A B ( E =
Cada uma das hastes de ligação AB e CD; são de aço( E = 200 G P a ) e tem seção transversal uniforme de 6,4 × 25,4m m . Determinar a maior carga que pode ser aplicada ao ponto E , sendo que a deflexão