Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 26
Cada uma das hastes de ligação AB e CD; são de aço e tem seção transversal uniforme de . Determinar a maior carga que pode ser aplicada ao ponto , sendo que a deflexão nesse ponto não pode exceder a
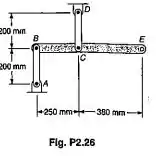
Passo 1
Vamos fazer um desenho esquemático da estrutura. Vamos dizer que existe uma carga no ponto que é o valor que queremos descobrir.
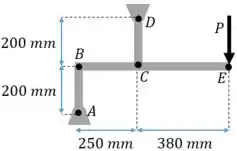
Para facilitar, vamos fazer uma seção deixando apenas a barra . Como nos pontos e temos apenas um pino conectado a uma barra, então as reações nesses pontos são forças no sentido das barras.
Então vamos calcular as reações em função de
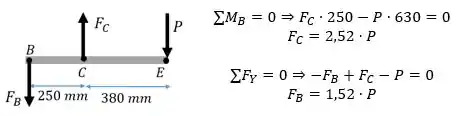
Passo 2
Temos que calcular a área de seção transversal das barras.
Passo 3
Note que as duas forças que calculamos são trações:
Utilizando a Equação 2.7 do livro, vamos calcular a deformação nas barras AB e CD.
Passo 4
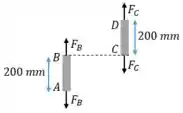
Vamos fazer um novo desenho. Nesse desenho vamos destacar em verde o alongamento das barras.
Utilizando as deformações do ponto B e C, podemos usar semelhança de triângulos para calcular a deformação no ponto E.
Vamos isolar a deformação do ponto E:
E aplicamos os valores:
Chegamos em:
A questão nos diz o valor máximo de
Chegamos no valor de