Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 23
Para a treliça de aço e carregamento mostrado, determinar as deformações nos membros e , sabendo-se que suas seções transversais tem e
Passo 1
A dificuldade dessa questão é encontrar as forças internas na treliça. Para isso vamos utilizar os conhecimentos da disciplina de Estática. Vamos desenhar a nossa estrutura e calcular as reações de apoio:
Primeiro usamos o somatório das forças na direção
E agora usamos o somatório de momentos no ponto :
E a somatória forças na direção
Passo 2
Vamos calcular a treliça pelo método dos nós:
Primeiro vamos pegar o nó
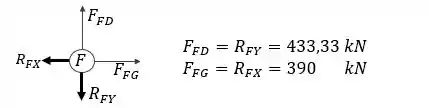
Nó G:
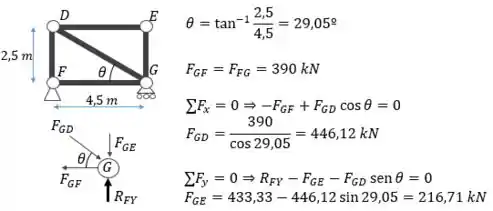
E agora vamos calcular o nó que é o que mais nos interessa:
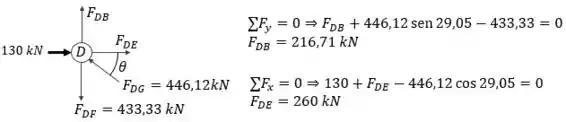
Passo 3
Agora temos todos as forças que nos interessam. Utilizando a Equação 2.5 do livro, vamos calcular a deformação nas barras DB e DE:
Resposta
Exercícios de Livros Relacionados
Para a montagem e o carregamento do Prob. 1.16, determine: (a) a tensão de cisalhamento média no pino A;(b) a tensão de esmagamento em A, na barra AB.Dados: diâmetro do pino = 15,2mm
Duas peças de madeira de seção transversal retangular uniforme de 76x127mm são unidas, através de uma emenda chanfrada e simplesmente colada, como indicado. Sabendo-se que P=3560KN, determine as tensõ
Um tubo de aço de 300mm de diâmetro externo é fabricado com chapa de 6,35mm de espessura, por meio de um cordão de solda ao longo de uma hélice que forma um ângulo de 22,5 ° com um plano perpendicular
Para o tubo do Prob.1.39, sabendo-se que as máximas tensões nas direções normal e tangencial, no cordão de solda são σ = 165 M P a e τ = 110 M P a , respectivamente, determine a intensidade da maior f
Para a montagem e o carregamento do Prob. 1.16, determine: (a) a tensão de cisalhamento média no pino C;(b) a tensão de esmagamento em C, na barra AB.(c) a tensão de esmagamento em B, na barra.Dados: