Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 18b
Um tubo cilíndrico de poliestireno de parede fina , com de espessura e uma placa rígida circular (é ostrada apenas parte dela), são usadas para suportar uma barra de aço , com de comprimento e de diâmetro. Seu uma carga de é aplicada em , determinar: (a) O alongamento da barra (b) a deflexão do ponto (c) a tensão normal na barra AB
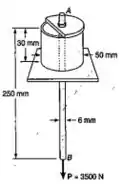
Passo 1
A gente já calculou o alongamento da barra . Um erro comum é acreditar que o alongamento da barra é igual a deflexão do ponto .
Mas note que, a barra AB se alonga, mas o cilindro de poliestireno é comprimido. Então, a deflexão do ponto B é resultado do alongamento da barra AB e da diminuição do cilindro de poliestireno.
A força que atua sobre o cilindro é a mesma que atua na barra:
Passo 2
Abaixo tem uma vista superior do cilindro:
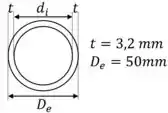
Vamos nos basear no desenho para calcular o diâmetro interno do cilindro:
E com isso podemos calcular a área de seção transversal do cilindro:
Passo 3
E agora vamos usar a Equação 2.7 para calcular o encurtamento do cilindro:
O carregamento é , o tamanho original do cilindro é , a área de seção transversal do cilindro é , e o módulo de elasticidade do cilindro é .
Não vamos esquecer de converter todas as unidades de medida:
Passo 4
Agora vamos calcular o deslocamento do ponto . Para isso, vamos somar a deformação do cilindro e a deformação da barra.