Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 206

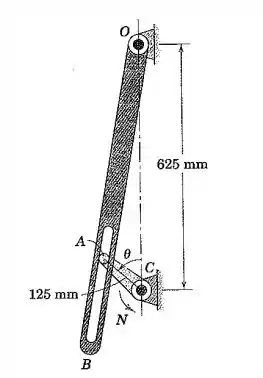
O braço ranhurado OB oscila em torno da vertical pela ação da manivela rotativa CA com 125 mm de comprimento, onde o pino A se acopla à ranhura. Para uma velocidade constante N = 120   r p m da manivela CA, determine e represente graficamente a velocidade angular β ˙ do braço OB como uma função de θ ao longo de 360 ° , onde β é o ângulo entre OC e OB. Encontre θ para a velocidade angular nula de OB.

Passo 1

Bom pessoal, esta questão é resolvida a partir de relações geométricas e trigonométricas. A figura da questão está representada aqui embaixo.

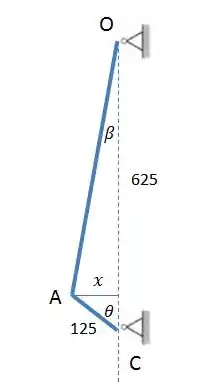
Podemos escrever o valor x das seguintes formas:

x = A C   s e n θ

x = 625 - A C   c o s θ t a n β

Igualando os temos:

A C   s e n θ = 625 - A C   c o s θ t a n β

125   s e n θ = 625 - 125   c o s θ t a n β      

s e n θ 5 -   c o s θ = t a n β           ( 1 )      

Como queremos saber a velocidade angular β ˙ , podemos derivar a equação acima para este termo aparecer (não esquecer da regra da cadeia):

d d t → 125 θ ˙   c o s θ = 125 θ ˙   s e n θ t a n β + 625 - 125   c o s θ β ˙ sec 2 ⁡ β

Vamos isolar agora o termo β ˙ :

β ˙ = 125 θ ˙   c o s θ - 125 θ ˙   s e n θ t a n β 625 - 125   c o s θ sec 2 ⁡ β = θ ˙   ( c o s θ -   s e n θ t a n β ) 5 -   c o s θ ( 1 + tan 2 ⁡ β )

β ˙ = θ ˙   ( c o s θ -   s e n θ t a n β ) 5 -   c o s θ ( 1 + tan 2 ⁡ β )

Agora temos a expressão de β ˙ em função de θ   e   d e   β . O valor de θ ˙ é dado no enunciado (N). Basta converter para a unidade rad/s.

θ ˙ = 120 2 π 60 = 4 π   r a d / s

Devemos agora deixar a expressão em função apenas de θ para poder plotar o gráfico. Para isto, vamos substituir o termo t a n β pela relação da equação (1):

β ˙ = 4 π c o s θ -   s e n θ s e n θ 5 -   c o s θ 5 -   c o s θ 1 + s e n θ 5 -   c o s θ 2

β ˙ = 4 π ( c o s θ -   s e n θ s e n θ 5 -   c o s θ ) 5 -   c o s θ + s e n 2 θ 5 -   c o s θ

Multiplicando em cima e embaixo por 5 -   c o s θ :

β ˙ = 4 π c o s θ 5 -   c o s θ -   s e n 2 θ 5 -   c o s θ 2 + s e n 2 θ

β ˙ = 4 π 5 c o s θ - cos 2 ⁡ θ -   s e n 2 θ 25 - 10 c o s θ + cos 2 ⁡ θ + s e n 2 θ

β ˙ = 4 π 5 c o s θ - 1 26 - 10 c o s θ

Agora você pode usar o Software que preferir para plotar o gráfico. Mas a cara dele vai ficar a seguinte:

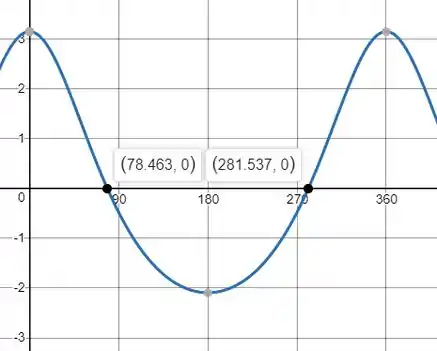
O β ˙ = 0 quando o gráfico corta o eixo horizontal θ . Então os valores do ângulo θ são:

  β ˙ = 0 → θ = 78,46 ° θ = 281,54 °

Resposta

  β ˙ = 0 → θ = 78,46 ° θ = 281,54 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma haste AB de 800 g é aparafusada a um disco de 1,2 kg. Uma mola de constante k = 12 N / m é fixada no centro do disco em A e na parede em C. Sabendo que o disco dobra sem deslizar, determine o perí
Duas hastes uniformes AB e CD, cada uma com comprimento l e massa m, são fixadas às engrenagens conforme mostrado. Sabendo que a massa da engrenagem C é m e que a massa da engrenagem A é 4m, determine
A haste 20-1b AB é conectada a dois discos de 8 lb conforme mostrado. Sabendo que os discos rolam sem deslizar, determine a frequência das pequenas oscilações do sistema.
Uma haste uniforme CD de 10 lb é soldada em C a um eixo de massa desprezível que é soldada aos centros de dois discos uniformes de 20 lb A e B. Sabendo que os discos rolam sem deslizamento, determine
Uma barra uniforme de comprimento L é suportada por um suporte esférico em A e por um fio vertical CD. Deduza uma expressão para o período de oscilação da barra se a extremidade B recebe um pequeno de