Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 207

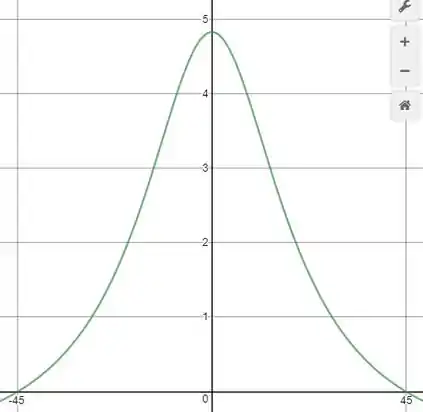
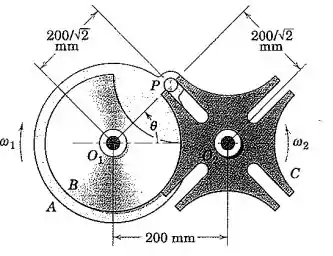
Para a roda de Genebra do Prob. 5/56, mostrada aqui novamente, escreva a expressão para a velocidade angular ω 2 da roda ranhurada C durante o acoplamento do pino P e represente graficamente ω 2 para o intervalo - 45 ° ≤ θ ≤ 45 ° .   A roda motriz A tem uma velocidade angular constante ω 1 = 2 r a d / s .

Passo 1

Bom pessoal, vamos dar uma passada rápida na resolução do Prob. 5/56. Veja a figura que representa o triângulo O 1 P O 2 , após um instante t qualquer:

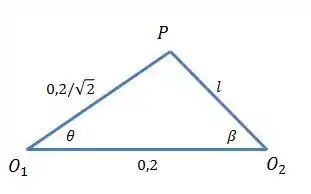
Pela lei dos Senos, temos as relações:

0,2 2   s e n β = 0,2 s e n π - θ - β

0,2 2   s e n β = 0,2 s e n θ + β

2 s e n β = s e n θ + β             ( 1 )

Como queremos saber a velocidade angular - β ˙   ( ω 2 ) , podemos derivar a equação acima para este termo aparecer (não se esquecer da regra da cadeia):

d d t → 2 β ˙   c o s β = θ ˙ + β ˙ c o s θ + β

Vamos isolar agora o termo β ˙ :

- β ˙ = ω 2 = θ ˙ c o s θ + β c o s θ + β - 2 c o s β         ( 2 )

Onde: θ ˙ = - 2   r a d / s

ω 2 = 2   c o s θ + β 2 c o s β - c o s θ + β         ( 3 )

Agora, abrindo o termo s e n θ + β da equação (1):

2 s e n β = s e n θ c o s β + s e n β c o s θ

t a n β = s e n θ 2 - c o s θ         ( 4 )

Agora você pode usar o Software que preferir para plotar o gráfico das equações (3) e (4). Mas a cara dele vai ficar a seguinte:

Resposta

ω 2 = 2   c o s θ + β 2 c o s β - c o s θ + β      

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma haste uniforme AB pode girar em um plano vertical em torno de um eixo horizontal em C localizado a uma distância c acima do centro de massa G da haste. Para pequenas oscilações, determine o valor
Duas hastes uniformes, cada uma com peso W = 1,2 lb e comprimento l = 8 pol., São soldadas para formar o conjunto mostrado. Sabendo que a constante de cada mola é k = 0,6 lb / in. e essa extremidade A
Uma barra AB esguia de 8 kg de comprimento I = 600 mm é conectada a dois colares de massa desprezível. O colar A está preso a uma mola de k = 1,2 kN / me constante e pode deslizar em uma haste vertica
Uma esfera A de 14 onças e uma esfera C de 10 onças estão presas às extremidades de uma haste de 20 onças AC, que pode girar em um plano vertical em torno de um eixo em B. Determine o período de peque
Um cursor de 5 kg pode deslizar sobre uma barra horizontal sem atrito e está ligado a uma mola de constante 550 N/m. Sobre ele atua uma força periódica de intensidade P = Pm sen ft, onde Pm = 15 N. De