Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 79

A barra uniforme com área da seção transversal A e massa por unidade de comprimento m está apoiada por um pino em seu centro. Se ela girar no plano horizontal a uma velocidade angular constante ω , determine a tensão normal média na barra em função de x .

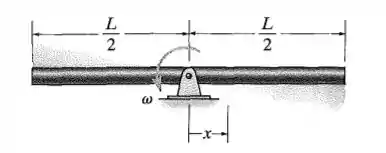
Passo 1

Desejamos calcular a tensão normal média em função da medida x mostrada na imagem. Lembrando que calculamos a tensão normal média como sendo

σ = N A

Onde

N : força normal no local onde queremos calcular;

A : Área transversal do local indicado;

Passo 2

Da segunda lei de Newton sabemos que a Força resultante é igual a aceleração vezes a aceleração que nesse caso é a aceleração angular ω dada por a n = ω ⋅ r 2 . Dessa forma, teremos

∑ F x = M ⋅ a n

M é a massa total do sistema que como foi dito no enunciado é m por unidade de comprimento. Então, vamos ter

N = m ⋅ L 2 - x ⋅ ω ⋅ x + 1 2 ⋅ L 2 - x

N = m ⋅ ω 8 ⋅ L 2 - 4 x 2

Sendo assim, nossa força normal será dada por

σ = N A = m ⋅ ω 8 A ⋅ L 2 - 4 x 2

Resposta

σ = m ⋅ ω 8 A ⋅ L 2 - 4 x 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A área da seção transversal da barra é 400 ⋅ 10 - 6 m 2 . Se ela estiver sujeita a uma carga axial distribuída uniformemente ao longo de seu comprimento e a duas cargas concentradas como mostra a figu
O pedestal suporta uma carga P em seu centro. Se a densidade de massa do material for ρ , determine a dimensão radial r em função de z de modo que a tensão normal média no pedestal permaneça constante
A sapata de apoio consiste em um bloco de alumínio de 150m m por 150m m que suporta uma carga de compressão de 6k N . Determine a tensão normal média e a tensão de cisalhamento média que agem no plano
Considere o problema geral de uma barra composta por m segmentos, cada um deles com área de seção transversal constante A m e comprimento L m . Se houver n cargas na barra como mostra a figura, escrev