Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 113
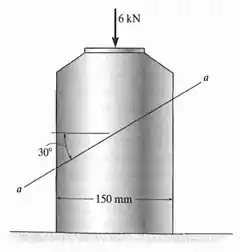
A sapata de apoio consiste em um bloco de alumínio de por que suporta uma carga de compressão de . Determine a tensão normal média e a tensão de cisalhamento média que agem no plano que passa pela seção . Mostre os resultados em um elemento de volume infinitesimal localizado no plano.
Passo 1
Oláaaa, querido! Tá bem?
Então, ele quer saber as tensões normal e de cisalhamento que atuam na seção .
E para isso a gente precisa da força interna de cisalhamento e da força normal. Para fazer esse tipo de questão, a primeira coisa é cortar nossa peça na seção que ele pediu, escolher um lado e fazer o diagrama de corpo livre da situação nova.
Vamos cortar nosso elemento em e olhar só para cima. Assim:
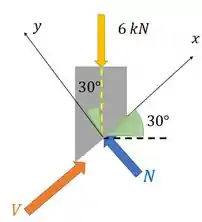
Aí percebe que a gente posiciona nessa seção vetores que representam essas forças internas. A força normal que deve ser perpendicular a seção , e a força de cisalhamento que deve ser paralela a seção.
O sentido dos vetores aqui é mais arbitrário mesmo, tá? Cê escolhe. O importante é respeitar os referenciais que escolher nas continhas. Vamos seguir!
Passo 2
Aplicando as equações de equilíbrio:
Já para o eixo :
Percebe que a gente colocou e na direção das forças que a gente queria porque aí só tivemos que decompor a força de .
Passo 3
Para achar as tensões na seção a gente também precisa da área da seção. Percebe que como a seção está inclinada, a gente precisa se esforçar mais um pouco para achar ela.
Um esqueminha da nossa peça cortada:
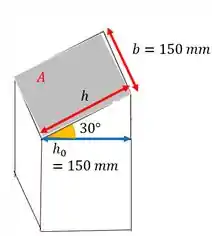
Aí por trigonometria a gente diz que
E a área da seção fica
Passo 4
Vamos ter que as tensões normais e de cisalhamento serão dadas por:
Assim, a única coisa que falta é substituirmos os valores aí:
Dica: quando a gente divide por , o resultado já sai lindão em 😊