Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 83
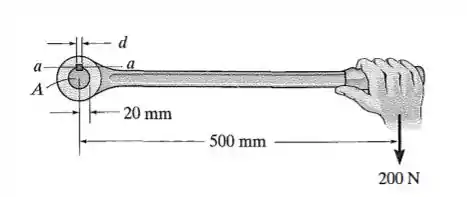
A manivela está presa ao eixo por uma chaveta e de . Se eixo for fixo e uma força vertical de for aplicada perpendicularmente ao cabo, determine a dimensão se a tensão de cisalhamento admissível para a chaveta for .
Passo 1
Queremos determinar o valor de dadas as condições descritas na imagem e no enunciado juntamente com o valor admissível de tensão de cisalhamento para esse caso em específico.
Passo 2
Podemos calcular o momento no ponto tomando o sentido anti-horário como positivo e vamos obter
Passo 3
Para a chave nós vamos ter
Resposta
Exercícios de Livros Relacionados
Para o estado plano de tensões mostrado, determinar a variação dos valores de θ , para que a intensidade de tensão de cisalhamento τ x ' y ' seja igual ou inferior que 45M P a .
Para o estado plano de tensões mostrado, determinar a variação dos valores de θ , para que a tensão normal σ x ' seja igual ou inferior que + 65M P a .
Para um estado plano de tensões é conhecido que, para cada uma das duas orientações indicadas para os eixos coordenados, as tensões, normal e de cisalhamento, são dirigidas como mostrado, e as intensi
Para um estado plano de tensões é conhecido que, para cada uma das duas orientações indicadas para os eixos coordenados, as tensões, normal e de cisalhamento, são dirigidas como mostrado, e as intensi
Resolver o Prob. 6.28, usando o círculo de Mohr.Uma força vertical de 4 k N é aplicada no ponto A de um componente de máquina mostrado. Determinar as tensões principais e a máxima tensão de cisalhamen