Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 73
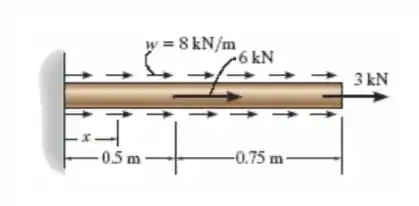
A área da seção transversal da barra é . Se ela estiver sujeita a uma carga axial distribuída uniformemente ao longo de seu comprimento e a duas cargas concentradas como mostra a figura, determine a tensão normal média na barra em função de para .
Passo 1
Queremos determinar a tensão normal média na barra mostrada na figura e para isso devemos lembrar, primeiramente, como se calcula a tensão normal que é dada pela seguinte fórmula
Com
P: resultante da força normal;
A: Área da seção transversal;
Passo 2
Na horizontal teremos uma força de reação indo da direita para a esquerda, a qual chamaremos de . Assim, fazendo o somatório das forças nessa direção vamos obter
Por fim, nossa tensão média será dada por
Resposta
Exercícios de Livros Relacionados
Os dois elementos usados na construção da fuselagem de um avião estão interligados por uma solda em boca-de -peixe a 30 ° . Determine a tensão de cisalhamento média e a tensão normal média no plano de
Um corpo de prova sob tração com área de seção transversal A é submetido a uma força axial P. Determine a tensão de cisalhamento média máxima no corpo de prova e indique a orientação θ de uma seção na
O corpo de prova falhou no ensaio de tração a um ângulo de 52° sob uma carga axial de 100 kN. Se o diâmetro do corpo de prova for 12 mm, determine a tensão de cisalhamento média e a tensão normal médi
A junta está submetida a uma força axial de 5k N . Determine a tensão normal média que age nas seções A B e B C . Considere que o elemento é liso e tem 50m m de espessura.
A junta de topo quadrada aberta é usada para transmitir uma força de 250 N e uma placa a outra. Determine as componentes da tensão de cisalhamento média e da tensão normal média que essa carga cria na