Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 84

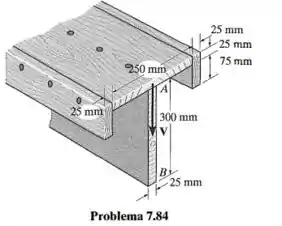
A viga é composta por quatro tábuas pregadas como ostra a figura. Determine a força de cisalhamento à qual cada prego ao longo dos lados C e da parte superior D deve resistir se estiverem uniformemente espaçados de s = 75 m m . A viga está sujeita a um cisalhamento V = 22,5   k N .

Passo 1

Dados da questão: V = 22,5   k N ,   s = 75   m m

A questão pede a força sobre os pregos: F p r e g o = ?

ESTRATÉGIA DE RESOLUÇÃO:

Primeiro vamos calcular o centroide e o momento de inércia da estrutura. Depois vamos calcular o momento estático nos pontos de interesse: a alma da viga e uma das abas. Por fim usaremos as equações de fluxo de cisalhamento para determinar a força sobre os pregos.

Passo 2

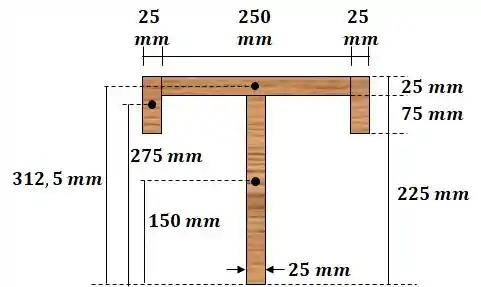
Calculamos o centroide da seção transversal:

y = ∑ A ⋅ y ∑ A

y = 25 ⋅ 3 0 0 ⋅ 15 0 + 2 ⋅ 100 ⋅ 25 ⋅ 2 7 5 + 250 ⋅ 25 ⋅ 312 , 5 25 ⋅ 300 + 2 ⋅ 100 ⋅ 25 + 250 ⋅ 25

y = 2 37,5   m m

Passo 3

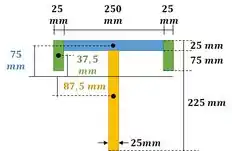
Podemos calcular o momento de inércia

I = I a z u l + I v e r d e + I a m a r e l o

I a z u l = 250 ⋅ 25 3 12 + 250 ⋅ 25 ⋅ 75 2 = 3 5,48 ⋅ 10 6 m m 4

I v e r d e = 2 ⋅ 25 ⋅ 100 3 12 + 25 ⋅ 100 ⋅ 37,5 2 = 1 1,2 ⋅ 10 6   m m 4

I a m a r e l o = 25 ⋅ 300 3 12 + 25 ⋅ 300 ⋅ 87,5 2 = 113,67 ⋅ 10 6   m m 4

I ≈ 1 60,35 ⋅ 10 6   m m 4

Passo 4

Vamos analisar primeiro a vista lateral. Vamos selecionar uma das abas para calcular o momento estático, já que primeiro queremos calcular o espaçamento dos pregos nas abas,

Q a b a = 25 ⋅ 100 ⋅ 37,5

Q a b a = 93750   m m 3

Passo 5

Para uma das abas, o cisalhamento do prego é simples, então o fluxo de cisalhamento sobre o prego é:

q = F p r e g o a b a s

E a fórmula do fluxo de cisalhamento é:

q = V Q a b a I

Igualando as expressões:

F p r e g o a b a s = V Q a b a I

Isolando o F p r e g o :

F p r e g o a b a = V Q a b a I s

Substituindo os valores:

F p r e g o a b a = 22,5   k N ⋅ 93750   m m 3 160,35 ⋅ 10 6   m m 4 ⋅ 75   m m

Valor da força sobre o prego das abas é:

F p r e g o a b a = 0,987   k N

Passo 6

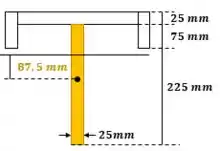
Calculamos agora o espaçamento dos pregos centrais. Pra isso precisamos do momento estático:

Q t a m p o = 25 ⋅ 300 ⋅ 87,5

Q = 656250   m m 3

Passo 7

Podemos calcular o   F p r e g o t a m p o de maneira similar ao feito anteriormente

F p r e g o t a m p o = V Q t a m p o I s

F p r e g o t a m p o = 22,5   k N ⋅ 656250   m m 3 160,35 ⋅ 10 6   m m 4 75   m m

F p r e g o t a m p o = 6,91   k N

Resposta

F p r e g o a b a = 0,987   k N

F p r e g o t a m p o = 6,91   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolver o Prob.5.40, considerando que a altura da placa é aumentada de 400m m para 600 m m .
Três pranchas são conectadas como mostrada, por parafusos de 16 m m de diâmetro e espaçados de 300m m , ao longo do eixo longitudinal da viga. Para uma força cortante vertical de 13350N , determinar a
Determinar a localização do centro de cisalhamento O de uma viga de parede fina de espessura uniforme e com a seção transversal mostrada.
Uma viga consiste em cinco pranchas de seção transversal 40x150 m m , conectadas por parafusos de aço, com espaçamento horizontal de 230m m . Sabendo-se que o cisalhamento na viga é vertical e igual a
Determinar a localização do centro de cisalhamento O de uma viga de parede fina de espessura uniforme e com a seção transversal mostrada.