Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.4 - Ex. 79
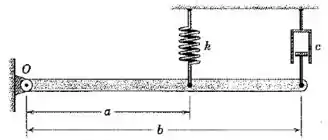
A barra uniforme de massa é livremente articulada em torno de um eixo horizontal que atravessa o ponto . Assuma pequenas oscilações e determine uma expressão para o fator de amortecimento . Para qual valor do coeficiente de amortecimento o sistema será criticamente amortecido?
Passo 1
Vamos começar montando uma expressão para o momento resultante em relação ao ponto :
Vamos fazer um diagrama para nos ajudar a calcular os momentos em relação ao ponto :
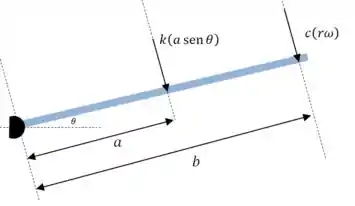
Obs.: O amortecedor mostrado no desenho fornece uma força do tipo . No desenho, nós reescrevemos .
Temos que multiplicar a magnitude de cada uma dessas forças pela sua distância perpendicular até o ponto :
E podemos aproximar , e lembrar que :
Passo 2
Agora vamos olhar para o outro lado da equação:
O momento de inércia do disco em relação ao ponto é tabelado:
Então:
Reorganizando um pouco:
Queremos uma expressão para o coeficiente de amortecimento . Vamos lembrar da forma geral da equação do oscilador harmônico:
Comparando as duas equações, podemos dizer que:
Substituindo a segunda equação na primeira:
Então:
Passo 3
Queremos achar para que o sistema seja criticamente amortecido, precisamos da seguinte igualdade:
Resposta
O fator de amortecimento é . E para ter amortecimento crítico, é preciso que .