Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.4 - Ex. 77

A casca cilíndrive com paredes finas de raio r e altura h é soldada ao pequeno eixo em sua extremidade superior conforme indicado. Determine a frequência circular natural ω n para pequenas oscilações do reservatório em torno do eixo y .

Passo 1

Vamos começar montando uma equação de momentos em relação ao ponto O marcado em vermelho na figura:

∑ M O = I O θ ¨

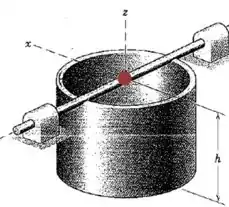
O centro de massa da casca cilíndrica está sobre o eixo z , e na metade da altura h . Ou seja, o centro de massa está a uma distância h 2 abaixo do ponto O .

Por isso, o momento da força peso em relação a O , quando o cilindro está deslocado por um ângulo θ será:

∑ M O = - m g h 2 sen ⁡ θ

Passo 2

Agora vamos olhar para o outro lado da equação:

∑ M O = I O θ ¨

O momento de inércia I O será o momento em relação ao eixo y . Podemos consultar isso em uma tabela para o caso de uma casca cilíndrica:

I O = 1 2 m r 2 + 1 3 m h 2

Então:

- m g h 2 sen ⁡ θ = 1 2 m r 2 + 1 3 m h 2 θ ¨

Agora vamos aproximar sen ⁡ θ ≅ θ e dividir tudo por m :

- g h 2 θ = 1 2 r 2 + 1 3 h 2 θ ¨

E então isolar θ ¨ :

θ ¨ + ( g h / 2 ) 1 2 m r 2 + 1 3 m h 2 θ = 0

O termo que está multiplicando θ é o quadrado da frequência natural do oscilador, então:

ω n 2 = ( g h / 2 ) 1 2 m r 2 + 1 3 m h 2

ω n = g h / 2 1 2 r 2 + 1 3 h 2

Resposta

A frequência natural para pequenas oscilações é ω n = g h / 2 1 2 r 2 + 1 3 h 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

54. O bloco de massa m = 45k g é suspenso por duas molas, cada uma com rigidez k = 3k N / m , e está sob a ação da força F = 350 ⋅ cos ⁡ 15 tN onde t é o tempo em segundos. Determine a amplitude X do
53. O corpo de 2,0k g está fixado a duas molas cada uma das quais com uma rigidez de 1,2k N / m . O corpo está montado sobre uma mesa vibratória que oscila harmonicamente na direção horizontal com uma
58. O disco circular de massa m está preso a um eixo elástico que está montado em um mancal rígido em A . Com o disco em repouso, uma força lateral P aplicada a ele produz uma deflexão lateral ∆ , de
57. Foi mencionado no texto que os valores máximos das curvas para o fator de amplificação M não estão localizados em ω / ω n = 1 . Determine uma expressão, em termos do fator de amortecimento ζ , par
55. Um sistema massa-mola com amortecimento viscoso é forçado harmonicamente na frequência natural não amortecida ( ω / ω n = 1 ). Se o fator de amortecimento ζ é duplicado de 0,1 para 0,2 , calcule a