Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.4 - Ex. 84
O mecanismo apresentado oscila no plano vertical em torno do pino . As molas, ambas de igual rigidez , estão comprimidas na posição de equilíbrio . Determine uma expressão para o período das pequenas oscilações em torno de . O mecanismo possui uma massa com centro de massa em , e o raio de giração do conjunto em relação a e .
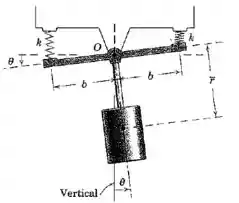
Passo 1
Vamos montar uma equação para os momentos em torno do ponto :
Começamos pelo momento da força peso:
E temos também o momento das forças elásticas exercido por cada uma das molas:
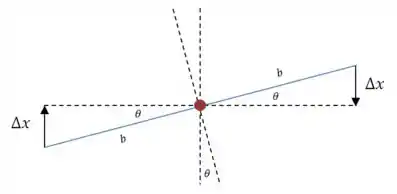
Perceba os dois momentos e tem sinal negativo, pois ambos favorecem o retorno ao ponto de equilíbrio.
Então:
Onde considearmos o momento das duas molas que seguram o “pêndulo”.
Passo 2
Agora vamos olhar para o outro lado da equação. O momento de inércia do sistema em relação ao ponto pode ser calculado com o raio de giração que foi dadoO
Então:
E podemos aproximar e :
E então a frequência angular natural do sistema é:
Com isso podemos calcular o período:
Resposta
O período de pequenas oscilações é .