Exercícios de Oscilações Forçadas - Lista de Exercícios Resolvida

Considere um corpo de massa , preso a uma mola ( de constante elástica e comprimento relaxado cuja outra extremidade presa está presa ao teto. Considere que pode oscilar, sem resistência, na vertical sob a ação de um campo gravitacional O corpo é solto, inicialmente em repouso, da posição em que a mola encontra-se relaxada.

1. DEDUZA a equação diferencial de movimento. Especifique CLARAMENTE o eixo e a origem de seu sistema de coordenadas.
2. Mostre que a equação diferencial de movimento pode ser escrita como a equação do oscilador harmônico simples em torno de uma nova posição de equilíbrio e determine esta posição.
3. Escreva a solução completa que descreve o movimento, em função dos dados do problema.

No sistema bloco-massa da figura, o bloco possui uma massa de e a mola possui massa desprezível. O sistema está sobre uma superfície sem atrito que faz um ângulo de com a horizontal.

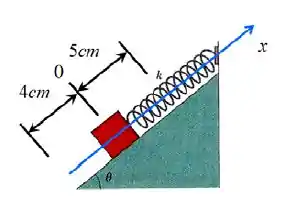
1. Sabendo que quando o sistema está em equilíbrio estático a mola sofre uma elongação de , calcule a constante da mola.
2. Em seguida, a mola é puxada mais e depois solta em . Encontre a frequência angular e o período .
3. Determine a equação de movimento, a velocidade e a aceleração.

Se necessário use e .

Considere duas molas, a mola 1 tem frequência natural enquanto a mola 2 tem frequência natural Ambas estão sob a ação de uma mesma força externa periódica que oscila com frequência A respeito da solução particular de ambas, podemos afirmar que:

1. Ambas oscilam em fase com a mesma frequência e mesma amplitude.
2. As molas oscilam defasadas mas com mesma frequência e mesma amplitude.
3. As molas oscilam em fase com mesma frequência e 2 apresenta uma amplitude maior que 1
4. A mola 2 oscila com maior amplitude e frequência que 1. Elas podem estar ou não em fase, dependendo das condições iniciais.
5. As molas oscilam fora de fase com mesma frequência e 2 apresenta uma amplitude maior do que 1.

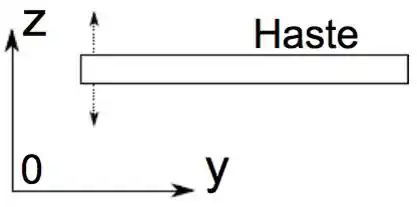
Um microscópio de força magnética usa a alta sensibilidade de uma haste micrométrica a variações de força para medir o gradiente de força magnética em uma região.

O movimento de oscilação da extremidade da haste se dá na direção perpendicular a haste, como ilustra a figura, e tem uma frequência angular própria . Para simplificar a questão, consideraremos a equação do movimento da extremidade da haste, sem força externa, da seguinte forma: . Um mecanismo permite excitar a haste com uma força de amplitude . A frequência angular é um pouco inferior a frequência angular própria da haste.

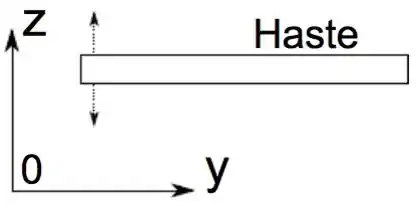
1. Escreva a equação diferencial de movimento do oscilador harmônico forçado. Considere que é a massa efetiva haste (massa em movimento durante as oscilações).
2. Escreva a solução da equação homogênea, a solução particular da equação inomogênea e a solução geral da equação inomogênea.
3. Suponha A PARTIR DE AGORA que uma força externa ADICIONAL atua sobre a haste. Como varia a frequência de ressonância se esta força adicional for tipo ?
4. Para uma excitação a uma frequência angular inferior a , como varia (qualitativamente) a amplitude com a presença da força ?

Um objeto de preso a uma mola, oscila sem atrito sujeito a uma força , conhecendo a constante elástica da mola, , obtenha o período e a amplitude do movimento.

Um bloco de massa desliza sem atrito sobre um plano inclinado que faz um ângulo com a horizontal e tem uma mola fixa no final da rampa. O bloco é solto de uma posição inicial tal que a distância entre a ponta livre da mola e a face do bloco é . Quando o bloco bate na mola, um dispositivo é acionado conectando o bloco na mola. O bloco comprime a mola até um valor máximo igual a , quando a velocidade instantânea do bloco torna-se zero. Considere um eixo ao longo do plano inclinado no sentido descendente e com sua origem na posição da ponta livre da mola quando ela não está deformada. Determine, em função dos parâmetros fornecidos e da aceleração da gravidade no local:

1. A frequência angular do movimento harmônico simples que o bloco executa após conectar-se à mola.
2. A posição na qual a velocidade do bloco é máxima.
3. A posição mais alta que o bloco alcança após conectar-se à mola.

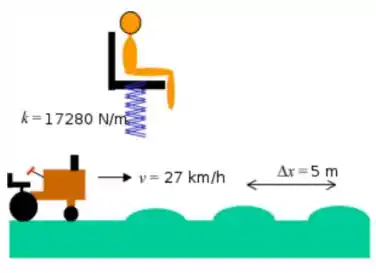
Considere um trator atravessando um campo onde existem ondulações em intervalos regulares. A distância entre cada monte é . Existe uma suspensão de mola ligada ao assento do motorista e este oscila em um regime no qual o amortecimento é desprezível. Podemos assumir uma mola de constante de mola , a massa do assento é e a do motorista é . O trator trafega a . Considere

1. Qual a frequência com que o trator passa em cada elevação?
2. Qual a frequência de oscilação natural do sistema assento-passageiro-mola?
3. Se considerar que, durante o trajeto, a força máxima aplicada pelo trator sobre o sistema cadeira-motorista é de , qual a amplitude máxima do movimento de oscilação do motorista?(assuma que a força é harmônica).
4. Para ocorrer o fenômeno de ressonância entre a força aplicada ao trator pelas ondulações e as oscilações sobre o sistema cadeira-passageiro, qual velocidade o trator deve atingir?(resposta em

Um microscópio de força magnética usa a alta sensibilidade de uma haste micrométrica a variações de força para medir o gradiente de força magnética em uma região.

O movimento de oscilação da extremidade da haste se dá na direção perpendicular a haste, como ilustra a figura, e tem uma frequência angular própria . Para simplificar a questão, consideraremos a equação do movimento da extremidade da haste, sem força externa, da seguinte forma: . Um mecanismo permite excitar a haste com uma força de amplitude . A frequência angular é um pouco inferior a frequência angular própria da haste.

1. Escreva a equação diferencial de movimento do oscilador harmônico forçado. Considere que é a massa efetiva haste (massa em movimento durante as oscilações).
2. Escreva a solução da equação homogênea, a solução particular da equação inomogênea e a solução geral da equação inomogênea.
3. Suponha A PARTIR DE AGORA que uma força externa ADICIONAL atua sobre a haste. Como varia a frequência de ressonância se esta força adicional for tipo ?
4. Para uma excitação a uma frequência angular inferior a , como varia (qualitativamente) a amplitude com a presença da força ?

Considere duas molas, a mola 1 tem frequência natural enquanto a mola 2 tem frequência natural Ambas estão sob a ação de uma mesma força externa periódica que oscila com frequência A respeito da solução particular de ambas, podemos afirmar que:

1. Ambas oscilam em fase com a mesma frequência e mesma amplitude.
2. As molas oscilam defasadas mas com mesma frequência e mesma amplitude.
3. As molas oscilam em fase com mesma frequência e 2 apresenta uma amplitude maior que 1
4. A mola 2 oscila com maior amplitude e frequência que 1. Elas podem estar ou não em fase, dependendo das condições iniciais.
5. As molas oscilam fora de fase com mesma frequência e 2 apresenta uma amplitude maior do que 1.

Um sistema composto por um bloco de massa que se encontra na horizontal, sobre uma mesa, e que está ligada à parede por uma mola, tem seu movimento representado por:

Onde as constantes estão em unidades SI. Despreze o atrito do bloco com a superfície da mesa.

1. Identifique a constante de amortecimento e a frequência angular na equação acima e determine o tipo de amortecimento sofrido pelo sistema.
2. Dado que o bloco se encontra inicialmente na posição , onde a origem deste sistema corresponde à posição do bloco com a mola relaxada, e com velocidade inicial determine a equação horária do sistema em função de sua amplitude e fase inicial.
3. Suponha agora que este sistema passe a oscilar sob a ação de uma força Ache a frequência angular sob qual a amplitude das oscilações é máxima. Assuma que o tempo é grande o suficiente para que a componente transiente do movimento já tenha sido totalmente suprimida. Encontre também esta amplitude máxima.

Um objeto de preso a uma mola, oscila sem atrito sujeito a uma força , conhecendo a constante elástica da mola, , obtenha o período e a amplitude do movimento.

Considerando o oscilador harmônico forçado não-amortecido no regime de ressonância (), que parte do repouso na posição de equilíbrio, qual o perfil da curva que passa pelos pontos de máximo da oscilação?

1. Linear decrescente
2. Exponencial decrescente
3. Constante
4. Linear crescente
5. Exponencial crescente

Um oscilador forçado sem amortecimento terá amplitude:

1. Dependente da frequência da força externa.
2. Que aumentará indefinidamente com o tempo.
3. Infinitamente grande já a partir do instante inicial, pois a energia não é dissipada.
4. Independente da frequência da força externa.
5. Nenhuma das Anteriores.

Um oscilador harmônico com amortecimento está em repouso na posição de equilíbrio quando é submetido a uma aceleração senoidal = ). Equação de movimento do tipo .

a) Sendo , qual a frequência da aceleração para que a amplitude final de oscilação (regime estacionário, ) seja máxima?

b) Mantendo-se a frequência anterior e reduzindo-se o amortecimento para , qual o aumento relativo da amplitude de oscilação final?

c) Qual o período do batimento que surge no início do movimento se e ?

d) Encontre a função que descreve o movimento em função do tempo, , durante o regime transitório com .

As partículas e da Figura abaixo estão ligadas uma à outra bem como a paredes verticais através de molas, todas elas de constante elástica . As partículas e estão fixadas nas paredes e não podem se movimentar. Inicialmente, as partículas (todas elas de massa ) estão na posição de equilíbrio, com as molas tendo um comprimento (que coincide com o comprimento natural). Aplica-se à partícula uma força horizontal , fazendo o sistema oscilar longitudinalmente. Seja , com o deslocamento da partícula em relação à posição de equilíbrio. Ao oscilar, cada partícula experimenta uma força de arrastro do ar proporcional à sua velocidade, sendo a constante de proporcionalidade.

PARTE I

Obtenha as equações que descrevem o movimento do sistema da Figura .

Obtenha as equações do movimento para as coordenadas normais e identifique-as freqüências naturais desses modos.

Obtenha a solução para as coordenadas normais (não é necessário especificar condições iniciais).

No sistema bloco-massa da figura, o bloco possui uma massa de e a mola possui massa desprezível. O sistema está sobre uma superfície sem atrito que faz um ângulo de com a horizontal.

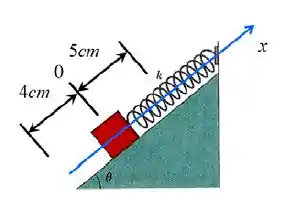
1. Sabendo que quando o sistema está em equilíbrio estático a mola sofre uma elongação de , calcule a constante da mola.
2. Em seguida, a mola é puxada mais e depois solta em . Encontre a frequência angular e o período .
3. Determine a equação de movimento, a velocidade e a aceleração.

Se necessário use e .

Um bloco de massa oscila preso a uma mola, de constante e comprimento natural na presença de um vento, cujo o efeito pode ser modelado como uma força constante:

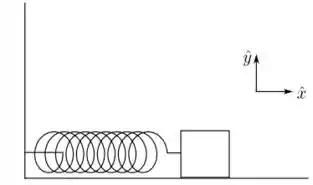
1. Escolha um sistema de coordenadas pra descrever esse movimento e diga onde está a origem. Usando esse sistema, obtenha a posição de equilíbrio do bloco.
2. Escreva a equação diferencial desse movimento supondo que não haja nenhum amortecimento.
3. Escreva a solução geral da equação acima para o caso
4. Escreva a função que descreve o movimento deste bloco , para , supondo que em a mola está com o comprimento natural e o bloco em repouso.

Um sistema oscilatório tem seu movimento descrito pela seguinte equação:

Onde e B são constantes, são frequências angulares e representa uma fase. Indique qual a afirmativa correta sobre o movimento na condição de ressonância, sabendo que o oscilador está inicialmente em repouso e na posição de equilíbrio:

(a) É uma oscilação sem amortecimento, com no qual a amplitude está crescendo.

(b) É uma oscilação sem amortecimento, com no qual a amplitude está decrescendo.

(c) É uma oscilação com amortecimento forte, com no qual a amplitude está decrescendo.

(d) É uma oscilação com amortecimento, com no qual a amplitude está decrescendo.

(e) É uma oscilação com amortecimento fraco, com no qual a amplitude está decrescendo lentamente.

Considere um corpo de massa , preso a uma mola ( de constante elástica e comprimento relaxado cuja outra extremidade presa está presa ao teto. Considere que pode oscilar, sem resistência, na vertical sob a ação de um campo gravitacional O corpo é solto, inicialmente em repouso, da posição em que a mola encontra-se relaxada.

1. DEDUZA a equação diferencial de movimento. Especifique CLARAMENTE o eixo e a origem de seu sistema de coordenadas.
2. Mostre que a equação diferencial de movimento pode ser escrita como a equação do oscilador harmônico simples em torno de uma nova posição de equilíbrio e determine esta posição.
3. Escreva a solução completa que descreve o movimento, em função dos dados do problema.

Uma massa de 4 kg, presa a uma mola de constante elástica k = 9N/m, inicialmente em repouso na condição de equilíbrio, recebe um impacto, que lhe transfere um impulso de , entrando em oscilação. Se a massa sofre um atrito viscoso , responda às questões:

a)Qual a função que descreve a o deslocamento x(t) do corpo em relação à condição de equilíbrio como x = 0? Justifique a expressão e os valores empregados.

b)Quando a dissipação do sistema é máxima? Qual o seu valor? Justifique sua resposta e quaisquer aproximações usadas.

c)Qual a energia potencial máxima do sistema? Em que instante ela ocorre? Justifique sua resposta e quaisquer aproximações usadas.

d)Se passarmos a excitar o sistema com uma força externa, qual a frequência de excitação da força externa aplicada à massa que produzirá a máxima amplitude de oscilação? Justifique.

Um corpo de massa está preso a uma mola de constante elástica O conjunto está colocado ao longo de um eixo em uma região na qual não há aceleração da gravidade, com a outra ponta da mola presa a uma superfície fixa. O corpo está em contato com um martelo e está também sujeita a uma força de resistência do ar dada por:

Para . O sistema é subcrítico, ou seja, temos onde e . Na situação de equilíbrio a superfície do corpo que está em contato com o martelo está na origem do eixo No instante o martelo imprime ao corpo uma velocidade dirigida no sentido positivo do eixo , e depois permanece fixo com a sua superfície de contato em Quando o corpo volta a se chocar com a superfície do martelo, que está em , ele se fixa ao martelo e permanece em repouso após este segundo choque.

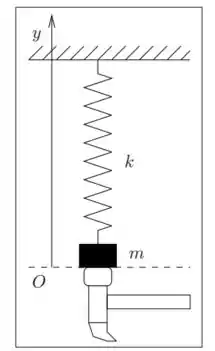
1. Determine a energia mecânica do sistema formado pelo corpo e pela mola em
2. Determine a posição e a velocidade no intervalo de tempo entre os dois choques.
3. Determine o tempo transcorrido entre os dois choques.
4. Determine a energia dissipada no segundo choque do corpo com o martelo.

Considere dois osciladores harmônicos simples, o oscilador 1 tem frequência natural enquanto o oscilador 2 possui frequência natural . Ambos estão sob a ação de uma mesma força externa periódica que oscila com frequência . A respeito da solução particular de ambos podemos afirmar que:

(a) Ambos oscilam em fase com mesma frequência e têm a mesma amplitude.

(b) Eles oscilam defasados mas com mesma frequência e mesma amplitude.

(c) Eles oscilam em fase com mesma frequência e 2 apresenta uma amplitude maior do que 1.

(d) O oscilador 2 oscila com maior amplitude e maior frequência do que o 1. Eles podem estar ou não em fase dependendo das condições iniciais.

(e) Eles os oscilam fora de fase com mesma frequência e 2 apresenta uma amplitude maior do que 1.

Considere o oscilador harmônico amortecido descrito pela equação diferencial

Qual a potência média fornecida pela força externa em uma oscilação?

Um corpo de oscila preso a uma mola que tem constante elástica igual a . A constante de amortecimento linear vale . O sistema é excitado por uma força senoidal de valor máximo igual a e frequência angular de . Qual é a amplitude das oscilações?

Um circuito eletrônico é formado por uma resistência elétrica, , por uma indutância, , por um capacitor, e por uma fonte alternada . A equação diferencial para a corrente elétrica, é

o que se mostra que o circuito se comporta como um oscilador harmônico forçado e amortecido.

1. Qual a frequência angular natural de oscilação da corrente, e o parâmetro de amortecimento, ?
2. Sendo

a solução estacionária, determine faça um esboço do gráfico de em função de .

3. Para , escreva a solução geral da equação diferencial dada acima.
4. Se as condições iniciais são e , determine a solução específica para este oscilador.

A respeito de um oscilador harmônico sujeito a uma força externa harmônica, podemos afirmar que:

Escolha uma opção:

A energia mecânica do oscilador é sempre constante

O oscilador sempre se moverá com a sua frequência angular natural, independente da força externa.

A amplitude do movimento do oscilador é independente da sua massa.

Se não houver amortecimento, a amplitude do movimento do oscilador tende a infinito quando a frequência da força externa tende a frequência natural do oscilador.

Se houver amortecimento, a amplitude do movimento do oscilador é sempre constante com o tempo.

O gráfico ao lado representa a equação horária de um oscilador, para um sistema que é composto por um bloco de massa preso a uma mola de constante elástica que está na posição vertical. Este sistema está imerso em um fluido viscoso com coeficiente de resistência e cuja força de resistência é proporcional à velocidade do corpo que se movimenta em seu interior. Dado que a velocidade inicial do móvel é , responda, sempre considerando o intervalo de tempo mostrado no gráfico:

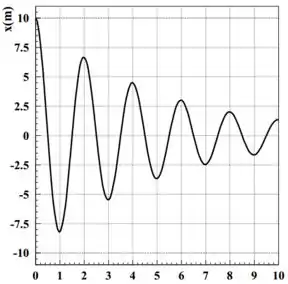
1. Dado o movimento do bloco no sistema descrito acima, qual a equação horária que descreve este sistema? Inclua os valores explícitos de suas constantes.
2. Determine a frequência natural e a constante da mola
3. Qual a velocidade do bloco no instante ?
4. Suponha agora que este mesmo sistema seja retirado do fluido viscoso e passe a oscilar num meio sem resistência. Neste novo regime, o deslocamento máximo é e a constante de fase é nula. Qual será a nova equação horária do sistema?

Três blocos de mesma massa m estão ligados a molas diferentes, de forma que suas frequências são . Estes blocos oscilam sem amortecimento, e são, a partir de um certo momento, submetidos às forças externas, todas estas com a mesma amplitude F0 e mesma frequência de oscilação de duas oscilações por segundo. Após terem atingido o regime estacionário, as amplitudes de seus movimentos obedecem às seguintes relações:

5. Nenhuma das alternativas

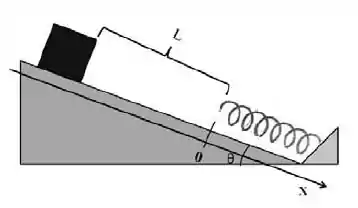
Um bloco de massa m, que pode deslizar sem atrito sobre um plano inclinado de um ângulo , está conectado ao topo do plano por uma mola ideal, que obedece à lei de Hooke, com constante elástica k e comprimento L quando não deformada.

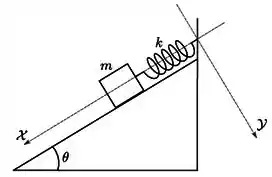
(a) Calcule a distância que o bloco se encontra do topo do plano inclinado na posição de equilíbrio.

(b) Deduza a equação de movimento do sistema, em termos da distância ao topo do plano inclinado.

(c) Resolva a equação de movimento, obtida no item anterior, para o caso do bloco ser solto do repouso a uma distância b, ao longo do eixo X indicado na figura, acima da posição de equilíbrio.

(Cap 13 - Ex 60) Uma força propulsora variando senoidalmente é aplicada a um oscilador harmônico amortecido de massa e constante da mola . Se a constante de amortecimento possui valor , a amplitude é quando a frequência angular da força propulsora é igual a . Em termos de , qual é a amplitude para a mesma frequência angular da força propulsora e a mesma amplitude da força propulsora quando a constante de amortecimento for: ? ?

O oscilador harmônico amortecido possui a seguinte equação de movimento

Supondo que o oscilador se encontra no regime subcrítico, assinale o valor da razão , onde é o período.

1. exp
2. exp
3. exp
4. exp
5. exp

Considere um oscilador harmônico não-amortecido na presença da força externa . Qual a solução geral para no regime de ressonância () sabendo que o oscilador se encontra inicialmente em repouso e na origem?

Um sistema de suspensão mecânica ideal de massa e constante elas´tica oscila sem amortecimento, sujeito à força externa da forma . Um estudo demonstra que, quando o sistema atinge o regime estacionário, a amplitude de oscilação do sistema em função da frequência angular da força externa se comporta como na figura ao lado. O valor da constante elástica dos sitema de suspensão é:

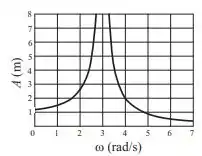
a) .

b) .

c) .

d) .

e) .

Um oscilador amortecido forçado, com , é colocado para oscilar a partir de duas condições iniciais distintas denominadas . O resultado dessas oscilações é graficado como versus t na figura abaixo.

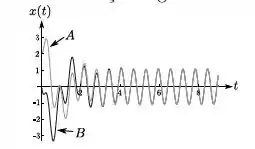
Marque a afirmativa correta:

1. As oscilações de no regime estacionário são iguais pois não dependem das condições iniciais.
2. As condições iniciais para A são .
3. As condições iniciais para são
4. As soluções transientes de são iguais pois não dependem das condições iniciais.
5. Somente está próximo da ressonância.

Uma pessoa está em pé sobre uma balança de banheiro que está sobre uma plataforma suspensa por uma grande mola. A plataforma executa um movimento harmônico simples vertical. Descreva a variação de leitura da escala da balança durante um período.

Uma cantoneira maciça é formada por duas barras delgadas idênticas, cada uma de massa M e comprimento L, conectadas perpendicularmente. Na junção entre as barras há um pequeno orifício circular de raio desprezível. O conjunto é pendurado por meio de um pino de suspensão passando pelo orifício e em torno do qual a cantoneira pode girar sem atrito, como mostrado na figura, numa situação em que o sistema está em equilíbrio.

Quando a cantoneira é deslocada ligeiramente para a direita ou para a esquerda, ela oscila no plano da figura

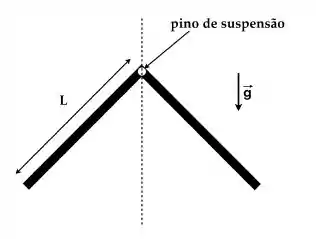
(a) Esboce o diagrama de forças externas que agem sobre a cantoneira num instante de tempo em que a linha que contém o CM desta faz um ângulo com a vertical.

(b) Adote um sistema de coordenadas com uma base de versores e determine o vetor torque total externo sobre a cantoneira na situação do item (a).

(c) No limite de pequenas oscilações, obtenha a equação diferencial para o ângulo , bem como a frequência natural das oscilações da cantoneira.

(d) Se o valor inicial para o ângulo é e a barra é liberada a partir do repouso, escreva a solução completa para o ângulo neste mesmo limite.

(e) Ainda no limite de pequenas oscilações, calcule as energias cinética e potencial da cantoneira como função do tempo. Verifique seu resultado, certificando-se de que a soma é constante. No limite de pequenos ângulos: