Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas de Revisão - Ex. 135
A barra uniforme BC tem uma seção transversal de área A e é feita de um aço doce que pode ser considerado elastoplástico com um módulo de elasticidade E e uma tensão de escoamento . Usando o sistema massa e mola mostrado na figura, deseja-se simular o deslocamento da extremidade C da barra à medida que a força axial P é gradualmente aplicada e removida, ou seja, os deslocamentos dos pontos C e C’ deverão ser os mesmos para todos os valor de P, Designando por o coeficiente de atrito entre o bloco e a superfície horizontal, determine uma expressa para (a) a massa m necessária para o bloco e (b) a constante k necessária para a mola.
Passo 1
E ai gurizada tudo belezinha? O enunciado pede que a gente determine a massa m necessária para o bloco e a constante k necessária para a mola. Para isso vamos esboçar um diagrama de corpo livre :D
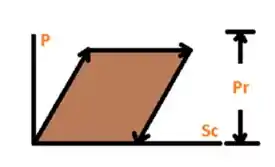
Diagrama de deflexão de força para o ponto C ou haste BC.
Para
Onde:
Digrama de deflexão de força para o ponto C do sistema de bloqueio e mola temos os seguintes somatório das forças.
Passo 2
Se o bloco não se mover, i e.,
Então
E se então desliza e ocorre.
E a força P é a remoção, a mola retorna ao seu comprimento inicial.
- Igualando e ,
- E a constante da mola temos:
Resposta
