Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas de Revisão - Ex. 124
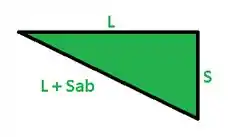
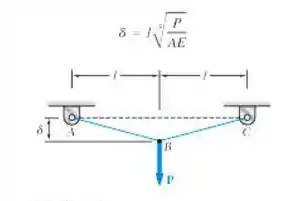
O fio uniforme ABC, de comprimento 2l quando não esticado, é preso aos suportes mostrados na figura de lhe é aplicada uma força vertical P no ponto médio B. Designando por A a área da seção transversal do fio e por E o módulo de elasticidade, mostre que, para , o deslocamento no ponto médio B é.
Passo 1
E ai gurizada tudo belezinha? O enunciado pede que a gente mostre que, para , o deslocamento no ponto médio B, então vamos começar a esboçar o diagrama de corpo livre.
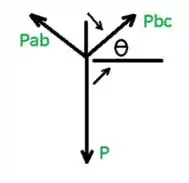
De acordo com o diagrama vamos considerar que:
Calculando o somatório das forças em Y temos:
E o alongamento é dado por:
Passo 2
Conforme nosso esboço de diagrama podemos considerar que:
